백준 22948 원 이동하기 2

이 문제는 트리를 구성하는 문제입니다.

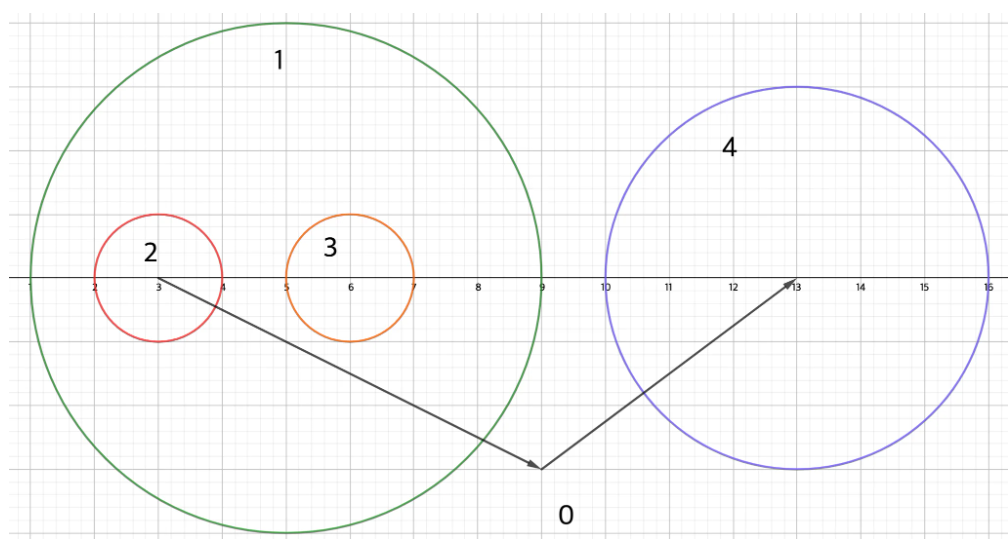
위 상황에 대해서 포함 관계를 기준으로 트리를 그리게 된다면

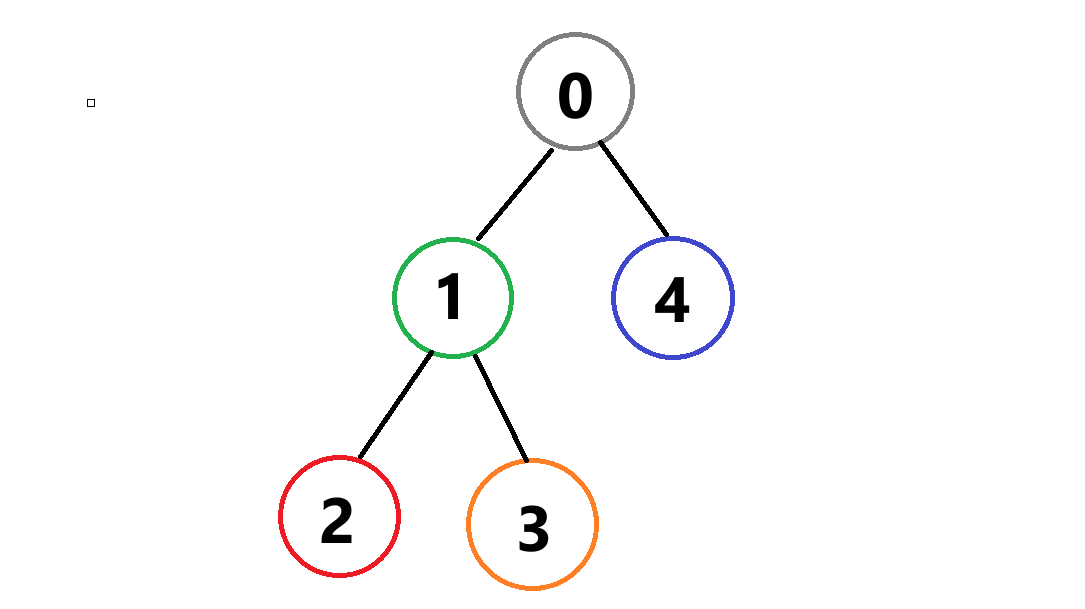
위와 같은 형태가 되고, 2->4로 가는 최단 경로는 2->1->0->4가 되는 것을 확인할 수 있습니다.

트리를 구성하는 방법

1. Greedy

트리 형태로 바꾸는 방법을 고민하다가 첫번째로 든 생각은 그리디였습니다.
반지름이 큰 순서로 배열을 정렬하고, 특정 노드가 다른 노드의 범위에 속해있는지 Brute force로 탐색하는 방법입니다.

하지만 N이 200,000이라는 제약 조건 때문에 $O(N^2)$의 시간복잡도는 적합하지 않다고 판단해서 넘어갔습니다.

2. Hash

hash자료구조를 통해 x의 범위 별로 어떤 노드에 속해있는지 판단하는 방법입니다.

시간복잡도 $O(Nx)$가 나오므로 너무 크다고 판단해서 넘어갔습니다.

3. Stack

괄호 닫기 문제와 유사하다고 판단하여 stack을 사용했습니다.
이 방법은 시간복잡도$O(N)$으로 해결할 수 있습니다.

원이 시작하는 좌표 또는 끝나는 좌표를 정렬합니다. 좌표가 작은 순서대로 탐색하며 다음 로직을 따라 처리합니다.

1. 원이 시작하는 좌표 : stack의 top의 원과 현재 원을 연결한다. stack에 원을 넣는다.

2. 원이 끝나는 좌표 : stack에서 pop연산을 수행한다.

코드는 다음과 같습니다.

struct Info{
    int num;
    int x;
    string status;

    Info(int num, int x, string status) : num(num), x(x), status(status){}

    bool operator<(const Info& I) const{
        return x > I.x;
    }
};
int main(){
	...
    for(int i = 0; i < N;i++) {
        int num, x, r;
        cin >> num >> x >> r;
        // 시작과 끝 좌표를 pq에 삽입 오름차순 정렬(정렬)
        pq.push(Info(num, x-r, "open"));
        pq.push(Info(num, x+r, "close"));
    }
    
    s.push(0);
    for(int i = 0;i < 2 * N;i++) {
        Info cur = pq.top();
        pq.pop();
        // 원이 시작하는 좌표
        if(cur.status.compare("open") == 0){
            connect(s.top(), cur.num);
            s.push(cur.num);
        }
        // 원이 끝나는 좌표
        else{
            s.pop();
        }
    }
    ...
}

최단 경로 탐색

트리를 구성하면 이제 최단 경로를 탐색해야 합니다.
다음과 같은 방법으로 구할 수 있다고 생각했습니다.

1. LCA (최소 공통 조상 알고리즘)

시작 노드와 목적지 노드 사이의 공통조상을 구한 뒤, 시작 -> 공통조상 ->목적지 까지의 경로를 출력하면 될 것 같습니다.

LCA의 시간복잡도는 $O(depth)$이므로 최소 $O(logN)$ 최대 $O(N)$으로 효율적인 방법입니다.

2. Dijkstra(다익스트라)

다익스트라를 통해 최단 경로를 찾는 방법도 좋을 것 같습니다.

$O(logN)$으로 효율적인 방법입니다.

3. DFS

저는 N이 200,000이므로 $O(N)$의 시간복잡도를 가지지만 구현 방법이 가장 단순한 DFS를 선택하여 구현했습니다.

전체 코드

#include<bits/stdc++.h>

using namespace std;

struct Info{
    int num;
    int x;
    string status;

    Info(int num, int x, string status) : num(num), x(x), status(status){}

    bool operator<(const Info& I) const{
        return x > I.x;
    }
};

priority_queue<Info> pq;
stack<int> s;
vector<int> connected[200'001];
bool visited[200'001];
vector<int> visiting;

void connect(int n1, int n2){
    connected[n1].push_back(n2);
    connected[n2].push_back(n1);
}

void DFS(int n, int end){
    visited[n] = true;
    visiting.push_back(n);
    if(n==end) {
        cout << visiting.size() << endl;
        for(int n : visiting) cout << n <<" ";
        cout << "\n";
    }
    for(int next : connected[n]){
        if(visited[next]) continue;
        DFS(next, end);
    }
    visited[n] = false;
    visiting.erase(visiting.end() - 1);
}

int main(){
    int N;
    cin >> N;
    for(int i = 0; i < N;i++) {
        int num, x, r;
        cin >> num >> x >> r;
        pq.push(Info(num, x-r, "open"));
        pq.push(Info(num, x+r, "close"));
    }
    
    s.push(0);
    for(int i = 0;i < 2 * N;i++) {
        Info cur = pq.top();
        pq.pop();
        if(cur.status.compare("open") == 0){
            connect(s.top(), cur.num);
            s.push(cur.num);
        }else{
            s.pop();
        }
    }

    int start, end;
    cin >> start >> end;
    

    // DFS
    DFS(start, end);
    

    return 0;
}