힙 Heap

힙 자료구조 : 우선순위 큐를 구현하기 위해 사용되는 자료구조 중 하나.

우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제한다는 특징이 있다. 따라서 데이터를 우선순위에 따라 처리하고 싶을 때 사용하면 된다. 파이썬에서는 일반적으로 동작시간이 더 빠른 heapq를 사용한다.

일반적으로 우선순위 큐 라이브러리에 데이터를 넣으면 첫번째 원소를 기준으로 우선순위를 설정한다. 따라서 (가치, 값)으로 넣어주면 된다.

우선순위 큐를 구현할 때는 내부적으로 최소 힙이나 최대 힙을 이용한다.

• 최소 힙 : 값이 낮은 데이터가 먼저 삭제 (파이썬 기본 힙 구조)
• 최대 힙 : 값이 높은 데이터가 먼저 삭제 (-> 최소 힙에 -를 붙여서 구현)

시간복잡도

• 삽입 : O(logN)
• 삭제 : O(logN)

메서드

라이브러리 추가

import heapq
heap = [] 

추가

• heapq.heappush(heap, item) : item을 heap에 추가. 첫번째 인자는 원소를 추가할 대상 리스트이며 두번째 인자는 추가할 원소.

삭제

• heapq.heappop(heap) : heap에서 가장 작은 원소를 pop & 리턴. 비어 있는 경우 IndexError가 호출.
• 만약 최솟값을 꺼내지 않고 리턴만 하려면 인덱스로 접근하기 (heap[0])

리스트 -> 힙 변환

• heapq.heapify(x) : 리스트 x를 즉각적으로 heap으로 변환함 (시간복잡도 O(N))

활용

최단 거리 알고리즘

최단 거리를 구하는 알고리즘(다익스트라)에서 거리가 짧은 노드 순서대로 큐에서 나올 수 있도록 할 때 우선순위 큐를 사용하면 편리하다.

n번째 최솟값 / 최댓값

최소 힙이나 최대 힙을 사용하면 n번째로 작은 값이나 n번째로 큰 값을 효과적으로 구할 수 있다.

n번째 최솟값을 구하기 위해서는 주어진 배열로 힙을 만든 후, heappop() 함수를 n번 호출하면 된다.

그러나 heapq 모듈에 이미 이러한 용도로 사용할 수 있는 nsmallest()라는 함수가 존재한다. nsmallest() 함수는 주어진 리스트에서 가장 작은 n개의 값을 담은 리스트를 반환하며 그 결과 리스트의 마지막 값이 n번째 작은 값이 된다.

from heapq import nsmallest

nsmallest(3, [4, 1, 7, 3, 8, 5])[-1]

반대로 n번째 최댓값을 구할 때는 nlargest() 함수를 사용한다.

from heapq import nlargest

nlargest(3, [4, 1, 7, 3, 8, 5])[-1]

힙 정렬

import heapq

def heap_sort(nums):
  heap = []
  for num in nums:
    heappush(heap, num)

  sorted_nums = []
  while heap:
    sorted_nums.append(heappop(heap))
  return sorted_nums

print(heap_sort([3, 1, 2, 8, 9, 5]))

프로그래머스 고득점 kit

Lv 2. 더 맵게

문제에 나와있는대로 차근차근 구현하면 되는 문제다. 우선순위 힙을 사용하면 빠르게 풀 수 있다.

import heapq
def solution(scoville, K):
    answer = 0
    heapq.heapify(scoville)
    
    now = scoville[0]
    # 맨 앞 음식 스코빌 지수가 K보다 낮고 뽑아낼 수 있으면
    while now < K and len(scoville) >= 2:
        heapq.heappush(scoville, heapq.heappop(scoville) + (heapq.heappop(scoville) * 2))
        answer += 1
        now = scoville[0]
    
    # 할 수 있는거 다 했는데 스코빌 지수가 K보다 작은 값이 존재한다면 만들 수 없는 경우
    if min(scoville) < K:
        return -1
    return answer

Lv 3. 디스크 컨트롤러

테케 5개 통과하는 슬픈 코드... 로직이 맞다는 생각이 드는데 수상하다. (물론 그러면 통과했겠지만...^.T)

import heapq
import math
def solution(jobs):
    answer = 0
    JOBS_LEN = len(jobs)
    
    jobs.sort() # 요청시간 기준 정렬
    
    heap = []
    t = 0 # 현재 시간
    
    for j in jobs:
        if t < j[0]:
            heapq.heappush(heap, (max(j[1], j[1]+j[0]-t), j[0], j[1]))
        else:
            heapq.heappush(heap, (j[1] - j[0] + t, j[0], j[1]))
    
    while jobs:
        result, j0, j1 = heap[0]
        
        # 하드디스크가 작업을 수행하고 있지 않을때
        if t < j0:
            idx = jobs.index([j0, j1])
            # 먼저 요청이 들어온 작업부터 처리해야함
            if idx != 0:
                j0, j1 = jobs[0]
                result = max(j1, j1 - j0 + t)
            t = max(t+j1, j0 + j1)
    
        else:
            t += j1
        
        answer += result
            
        jobs.remove([j0, j1])
        jobs.sort()
        
        heap = []
        
        for j in jobs:
            if t < j[0]:
                heapq.heappush(heap, (max(j[1], j[1]+j[0]-t), j[0], j[1]))
            else:
                heapq.heappush(heap, (j[1] - j[0] + t, j[0], j[1]))
                
    return math.floor(answer / JOBS_LEN)

심지어 내가 생각한 로직대로 손계산한거랑 코드 돌아간 결과가 같은데 예상 답안과 다르다...^^ 문제 이해를 잘못한것같다.

테케는 이걸 썼다.

[[0, 6], [2, 8], [3, 7], [7, 1], [11, 11], [19, 25], [30, 15], [32, 6], [40, 3]] # 19

다른 사람의 풀이(출처)를 보고 고쳤다. 너무 복잡하게 생각했다. 그리고 현 상황에 실행할 수 있는 디스크가 없을 때를 고려하지 않았다.

풀이

1. 현재 시점 time에서 처리 가능한 작업이 있는 경우에는 힙에 넣어준다.
   힙에 넣을 때는 소요시간이 짧은 요소가 먼저 나올 수 있도록 순서를 (소요시간, 요청시간)으로 넣어준다.

   • 처리 가능한 작업 판단 여부 : 요청시간이 직전에 완료된 디스크의 시작 시간 start보다 크고 현재시간 time 이하인 경우

2. 처리할 디스크가 존재한다면 힙에서 뽑아 처리해준다.
   
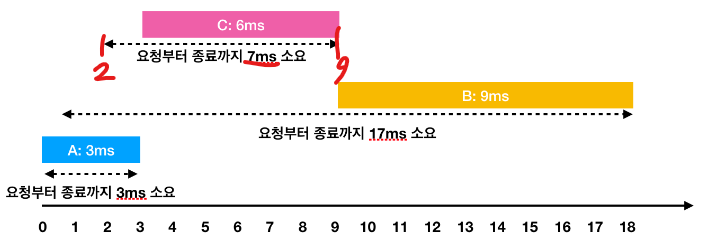
   어떻게 시간을 계산하는지 answer += (time - disk[1])는 위의 그림 참고.

3. 처리할 디스크가 없다면, 현재 시점 time에서 처리 가능한 디스크가 없는 것이므로 시간을 +1 증가시켜준다.

import heapq

def solution(jobs):
    answer, time, count = 0, 0, 0
    start = -1
    heap = []
    
    while count < len(jobs):
        for j in jobs:
            if start < j[0] <= time:
                heapq.heappush(heap, [j[1], j[0]]) # 소요시간 작은 것이 우선순위up
        
        # 처리할 디스크 존재
        if len(heap) > 0:
            disk = heapq.heappop(heap)
            start = time
            time += disk[0] # 소요시간 더해주기
            answer += (time - disk[1]) # 요청한 시간만큼 빼주기
            count += 1 # 처리한 디스크 수 증가
        
        # 현시점(time) 처리할 수 있는 디스크 없음, 시간 증가
        else:
            time += 1
            
    return int(answer / len(jobs))

Lv 3. 이중우선순위 큐

야매로... 리스트 정렬해서 풀었다. 효율성이 아예 없어서 가능했던 것 같다.

사실 최대 힙, 최소 힙 2개의 힙을 갖고 있으면서 동기화시켜보려다가 너무 지쳐서 리스트로 풀어봤더니 되서 허망했다. 문제 의도대로 푼 다른 사람의 코드를 보고 더 공부해야겠다.

# 이건 리스트로 푼 코드
def solution(operations):
    answer = []
    numbers = []
    for operation in operations:
        op, num = operation.split(" ")
        num = int(num)
        
        if op == "I":
            # 숫자 넣기
            numbers.append(num)
            numbers.sort()
        else:
            if len(numbers) != 0: # 뺄 수 있는 경우에만
                if num == -1: 
                    # 최솟값 빼기
                    numbers.pop(0)
                else:
                    # 최댓값 빼기
                    numbers.pop()
    
    if len(numbers) == 0:
        answer = [0,0]
    else:
        answer= [max(numbers), min(numbers)]
        
    return answer

어우 너무 좋은 코드를 찾았다. 짱이다... 나도 이렇게 풀고 싶다 출처

최소힙과 최대힙을 동기화시켜주기 위해 힙에 푸시할 때 입력받은 값 외에도 식별자 id을 하나 더 넣어준다. 삽입 연산 시에는 따로 동기화가 필요 없음. 각각 삽입만 해주면 끝!
삭제 연산 시에는 id를 기준으로 해당 노드가 다른 힙에서 삭제된 노드인가 아닌가를 판단한다. 이미 삭제된 노드일경우 삭제되지 않은 노드가 나올 때 까지 모두 버린다. 이후 삭제 대상 노드가 등장하면 삭제한다. 이를 위해 각 id별로 활성상태를 기록하는 플래그 리스트인 visited를 사용한다.

모든 연산이 끝난 후에도 이런 쓰레기 노드들이 들어있을 수 있어 결과를 내기 전 쓰레기 노드를 모두 비우고 리턴한다.

import heapq

def solution(operations):
    answer = []
    minq, maxq = [], []

    # 각 id별로 활성상태를 기록하는 플래그 리스트
    visited = [False for _ in range(1000001)]

    i = 0 # 식별자 id
    for operation in operations:
        op, num = operation.split(" ")
        num = int(num)

        if op == "I":
            heapq.heappush(minq, (num, i))
            heapq.heappush(maxq, (-num, i))
            visited[i] = True
        elif num == -1:
            # 삭제연산 시, id를 기준으로 해당 노드가 다른 힙에서 삭제된 노드인지 체크
            # 이미 삭제된 노드일경우 삭제되지 않은 노드가 나올 때까지 버림
            while minq and not visited[minq[0][1]]:
                heapq.heappop(minq)
            # 삭제 대상 노드가 등장하면 삭제
            if minq:
                visited[minq[0][1]] = False
                heapq.heappop(minq)
        else:
            while maxq and not visited[maxq[0][1]]:
                heapq.heappop(maxq)
            if maxq:
                visited[maxq[0][1]] = False
                heapq.heappop(maxq)

        i += 1
    
    # 모든 연산이 끝난 후에도 쓰레기 노드들이 들어 있을 수 있어 비우기
    while minq and not visited[minq[0][1]]:
        heapq.heappop(minq)
    while maxq and not visited[maxq[0][1]]:
        heapq.heappop(maxq)

    if len(minq) == 0:
        answer = [0,0]
    else:
        answer= [-heapq.heappop(maxq)[0], heapq.heappop(minq)[0]]
    
    return answer

문제를 빠르게 이해하고 로직을 짜는 것에 더 익숙해져야겠다. 레벨 3부터는 확실히 코드가 길어지거나 로직을 제대로 잡지 못하면 1~2시간 내에 못 푸는 경우가 많았다. 프로그래머스 레벨 3 문제들을 1시간 30분 ~ 2시간 안에 무난하게 풀 수 있을 때까지 달려보자.