그리디 알고리즘
탐욕법이라고도 하는 그리디(Greedy) 알고리즘은 “현재 상황에서 최적이라고 생각하는 해를 선택“하는 방법이다.
그러나 말그대로 앞으로 남은 선택들을 고려하지 않고 현재 상황만 고려하기 때문에 항상 최적해(Global optimum)를 보장하지는 않는다.
그리디 알고리즘의 정당성
그리디 알고리즘으로 최적해를 도출하기 위해서는 아래 두가지 조건을 만족해야 한다.
-
탐욕적 선택 속성 (greedy choice property)
탐욕적인 선택이 항상 안전하다는 것이 보장된다는 의미이다. 즉, 그리디한 선택이 언제나 최적해를 보장해야한다. -
최적 부분 구조 (optimal substructure)
부분 최적해(Local optimum)들이 모여 전체 최적해(Global optimum)를 구할 수 있는 경우이다. 즉, 전체 문제가 여러 부분 문제로 분할되며, 이 단계 하나하나에 대한 최적해가 도출되어야 한다는 의미이다.
프로그래머스 고득점 kit
Lv 1. 체육복
체육복을 잃어버린 lost 배열과 여벌 체육복이 있는 reserve 배열을 보면서 총 체육복의 개수 배열 cloth를 생성했다. 이 배열을 보면서 만약 해당 학생이 앞이나 뒤 학생에게 줄 수 있으면 건네주면 된다.
그리디는 이 문제가 그리디인지 판단하는 게 관건이다... 많이 풀어서 감을 익히는 것이 중요하겠다.
def solution(n, lost, reserve):
answer = 0
cloth = [1] * (n+1) # 1번부터 n번까지 체육복을 갖고 있는 학생들
cloth[0] = 0
for i in lost:
cloth[i] -= 1
for i in reserve:
cloth[i] += 1
for i in range(1, len(cloth)):
if cloth[i] == 2:
if i-1>=1 and cloth[i-1] == 0:
cloth[i] -= 1
cloth[i-1] += 1
elif i+1<len(cloth) and cloth[i+1] == 0:
cloth[i] -= 1
cloth[i+1] +=1
for i in cloth:
if i > 0:
answer += 1
return answerLv 2. 조이스틱
그리디라기에는 완탐에 가까운 문제였다. 테케는 통과하는데 실제로 제출해보니 우수수 틀려서 해설을 참고했다.
조이스틱의 상하 이동은 최적화를 시킬 수 없으니, 좌우 이동을 최솟값으로 가져가야 한다. 기본적으로 가장 적게 이동하는 방법은 첫번째 커서에서 마지막 커서까지 오른쪽으로 쭉 이동하는 것 len(name)-1이다. 그러나 만약 연속된 A가 등장한다면 이를 지나가지 않는 것도 고려해야 한다.
따라서 현재 글자의 다음 글자부터 연속된 A가 등장한다면, 해당 연속된 A를 지나가지 않도록 2가지 시나리오를 고려할 수 있다.
- 연속된 A의 왼쪽까지만 오고 되돌아가기
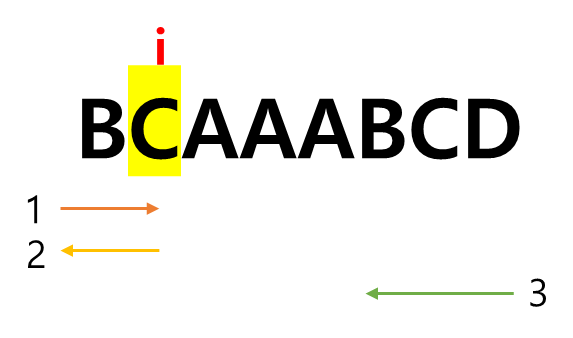
이 경우에는 2 * i + len(name) - next 가 된다.
- 뒤에서부터 연속된 A의 오른쪽까지만 오고 되돌아가기
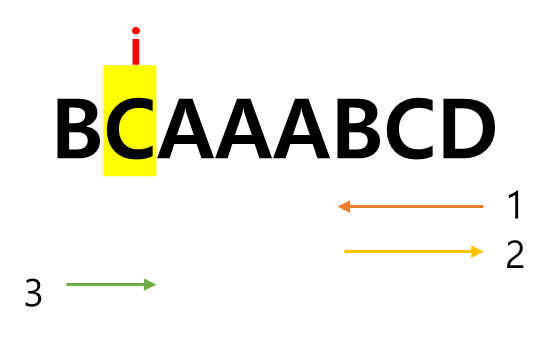
이 경우에는 i + 2 * (len(name) - next)가 된다.
매번 최솟값을 갱신해주며 끝까지 살펴보면 된다. 최종적인 코드는 다음과 같다.
def solution(name):
answer = 0
min_move = len(name) - 1
for i, v in enumerate(name):
if v != "A":
answer += min(ord(v) - ord("A"), ord('Z') - ord(v) + 1)
# 현재 문자열 다음으로 연속된 A 문자열 찾기
next = i + 1
while next < len(name) and name[next] == 'A':
next += 1
min_move = min([min_move, 2 *i + len(name) - next, i + 2 * (len(name) -next)])
answer += min_move
return answerLv 2. 큰 수 만들기
1시간정도 풀면서 분명 방향은 맞게 잡은 것 같은데 테케만 딱 통과해서 해설을 참고했다.
stack으로 접근했고, 큰 수가 되려면 스택의 마지막 값이 넣어줄 값보다 작다면 크거나 같은 값이 나올 때까지 값들에 대해서 pop을 해줘야 한다. ( 시간 복잡도 : O(n) )
다만 자르는 k개를 다 사용하지 않은 경우 뒤에서부터 k개만큼을 잘라줘야하는데 이는 리스트의 슬라이싱을 사용했다. [:-k]는 뒤에서부터 k개를 자르는 것을 의미한다.
def solution(number, k):
answer = ''
nums = []
for n in number:
if len(nums) == 0:
nums.append(int(n))
continue
if k > 0:
while nums[-1] < int(n):
nums.pop()
k-= 1
if len(nums) == 0 or k <= 0:
break
nums.append(int(n))
answer = ("".join(map(str, nums)))
if k>0:
answer = answer[:-k]
return answer코드를 한번 정리했다. 생각해보니 숫자는 두자리가 등장할 일이 없으니 굳이 매번 정수로 바꿔줄 필요가 없었다. 문자열 숫자도 0~9 사이는 맞게 비교가 되니까!
def solution(number, k):
answer = ''
nums = []
for n in number:
if len(nums) == 0:
nums.append(n)
continue
while nums and k>0 and nums[-1] < n:
nums.pop()
k-= 1
nums.append(n)
answer = ("".join(map(str, nums)))
if k>0:
answer = answer[:-k]
return answerLv 2. 구명보트
이 문제.. 제법 잘 풀었다. 기특하다.
구명보트를 최대한 적게 써서 다 탈출시켜야 하며, 구명보트에는 최대 2명이 탑승할 수 있다.
구명보트를 적게 쓰기 위해 일단 사람의 무게 people을 정렬한다. people의 첫번째 요소를 뽑은 뒤, 끝에서부터 같이 탈 수 있는 인원을 체크한다. 만약 첫번째 사람과 같이 탈 수 없으면 어차피 끝의 그 사람은 혼자 타야한다. (현 시점에서 제일 가벼운 사람과 못 타기 때문에)
따라서 같이 탈 수 있는 사람이 등장하기 전까지 혼자 타야되는 사람 수를 빼주고, 같이 탈 수 있는 인원은 한 배에 태우도록 알고리즘을 짰다.
from collections import deque
def solution(people, limit):
people.sort()
q = deque(people)
boat = 0
while q:
first = q.popleft()
boat += 1
alone = 0
together = 0
for i in range(len(q)-1, -1, -1):
if q[i] + first > limit:
alone += 1
else:
together += 1
break
for i in range(alone):
q.pop()
boat += 1
if together != 0:
q.pop()
return boatLv 3. 섬 연결하기
시도한 방법
- 노드의 비용을 기준으로 정렬한 뒤 가장 적은 비용의 길을 각 노드에서 선택하는 방식으로 코드를 짰다
-> 테스트케이스만 통과하고 실제로는 전부 FAIL
각 노드를 돌면서 방문하지 않은 노드 기준으로 최솟값인 경우에만 방문하도록 했는데 ... 쩝 아니었다. 아쉬우니 코드는 첨부.
def solution(n, costs):
answer = 0
graph = [[] for _ in range(n)] # graph[x] = [(node, cost), (), ...]
for x, y, c in costs:
graph[x].append((y, c))
graph[y].append((x, c))
# 비용 순으로 각 그래프 노드 정렬
for i in range(len(graph)):
graph[i].sort(key=lambda x: x[1])
visit = [False] * (n)
def dfs(start):
nonlocal answer
if visit[start]:
return
visit[start] = True
for node, cost in graph[start]:
if not visit[node]:
# 방문X 노드 중 최솟값인 경우에만 방문하도록
if graph[node][0][0] == start:
answer += cost
dfs(node)
dfs(0)
return answer해설을 찾아보니 그리디 알고리즘의 일종인 크루스칼 알고리즘으로 풀어야 한다고 한다. 이를 위해 잠깐 필요한 개념을 정리했다.
서로소 집합 자료구조
- union : 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 것 (합집합)
- find : 특정 원소가 속한 집합이 어떤 집합인지 알려주는 것
트리 자료구조를 이용하여 집합을 표현하며 서로소 집합 계산 알고리즘은 다음과 같다.
- union 연산을 확인하여, 서로 연결된 두 노드 A, B를 확인한다.
1-1. A와 B의 루트 노드 A'와 B'를 각각 찾는다.
1-2. B' -> A' 되도록 연결한다 (보통 더 작은 노드가 부모가 되도록 함) - 모든 union 연산을 처리할 때까지 1번 과정을 반복한다.
union 연산을 효과적으로 수행할 수 있도록 부모 테이블을 항상 가지고 있어야 한다. 또한 루트 노드를 즉각적으로 계산할 수 없고 재귀적으로 부모 테이블을 확인하며 거슬러 올라가야 한다.
신장 트리 Spanning Tree
- 신장 트리 : 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
신장 트리 중 최소 비용으로 만들 수 있는 신장 트리를 찾는 알고리즘을 최소 신장 트리 알고리즘이라고 한다. 대표적인 최소 신장 트리 알고리즘은 크루스칼 알고리즘이 있다.
크루스칼 알고리즘
가장 적은 비용으로 모든 노드를 연결할 수 있는 알고리즘. 그리디 알고리즘으로 분류된다.
먼저 모든 간선에 대해 정렬을 수행한 뒤 가장 거리가 짧은 간선부터 집합에 포함시키면 된다. 이때 사이클을 발생시킬 수 있는 간선의 경우, 집합에 포함시키지 않는다.
자세한 알고리즘의 구현은 다음과 같다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
2-1. 사이클이 발생하지 않는 경우, 최소 신장 트리에 포함
2-2. 사이클이 발생하는 경우, 최소 신장 트리에 포함X - 모든 간선에 대해서 2번의 과정 반복
크루스칼 알고리즘을 사용하여 푼 소스코드는 다음과 같다.
def solution(n, costs):
# 특정 원소가 속한 집합 찾기 (루트 노드 찾기)
def find_parent(parent, n):
if parent[n] != n:
# 부모 찾을 때까지 재귀적으로 호출
parent[n] = find_parent(parent, parent[n])
return parent[n]
# 두 원소가 속한 집합 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
answer = 0
costs.sort(key=lambda x: x[2]) # 비용 기준으로 오름차순 정렬
parent = [i for i in range(n)] # 부모 테이블, 부모를 자기 자신으로 초기화
for a, b, cost in costs:
# 사이클 존재X
if find_parent(parent, a) != find_parent(parent, b):
# 연결하고 비용 계산
union_parent(parent, a, b)
answer += cost
return answer위의 방식으로 직접 union, find 함수를 작성하는 것 외에 더 간단한 방법도 구글링하니 찾아서 공부를 위해 기록한다!
def solution(n, costs):
answer = 0
costs.sort(key = lambda x: x[2]) # 비용 기준으로 오름차순 정렬
connect = set([costs[0][0]]) # 연결을 확인하는 집합
# Kruskal 알고리즘으로 최소 비용 구하기
while len(connect) != n:
for cost in costs:
if cost[0] in connect and cost[1] in connect:
continue
if cost[0] in connect or cost[1] in connect:
connect.update([cost[0], cost[1]])
answer += cost[2]
break
return answerconnect는 연결된 섬을 확인하는 집합으로 섬이 중복되면 안되므로 리스트가 아닌 집합을 사용한다.
반복문으로 costs를 돌면서 두 섬이 connect에 있으면 넘어가고 두 섬 중 하나만 있는 경우 두 섬을 connect에 추가해주고 answer에 비용을 추가한다.
set 자료형에서 update는 여러 개의 값을 추가할 수 있도록 해주는 메서드이다. 메서드에 추가하고자 하는 값을 담은 배열을 넘겨주면 된다.
Lv 3. 단속카메라
꽤 많이 정답에 접근했는데 시간이 4~50분이 걸려도 테케만 통과하고 실제 코드는 아예 통과를 못해서 풀이를 참고했다. 거의 맞게 접근했건만...! 너무 빙빙 돌려서 생각했다.
어렵게 생각할 것 없이, 진출시점을 기준으로 정렬하여 진출 위치마다 카메라를 갖다 놓으면 된다. (진출시점routes[1] 으로 정렬을 해야 모든 차량을 놓치지 않는다)
만약 카메라 위치보다 진입 위치가 더 크다면 카메라가 해당 차량을 잡을 수 없는 것이므로 카메라 대수를 +1 해주고 카메라 위치를 최대한 뒤(진출위치)로 설정한다.
헤맨 것에 비해 실제 완성된 코드가 굉장히 간결해서 조금 슬펐다. 나는 불필요한 삽질을 한 것이었구나...
def solution(routes):
answer = 0
routes.sort(key=lambda x: x[1]) # routes를 차량이 나간 지점 (진출) 기준으로 정렬
camera = -30001 # -30001로 초기 데이터 설정
for start, end in routes:
if camera < start:
answer += 1 # 단속할 수 없는 위치에 있는 것이므로 카메라 설치
camera = end # 최대한 뒤(진출 위치)에 카메라 설치
return answer