시간복잡도

일반적으로 1억번(100,000,000 = 10^8)의 연산 = 1초의 실행시간
(당연한건데 자꾸 헷갈려서.. 4개단위로 끊어서 보자고)

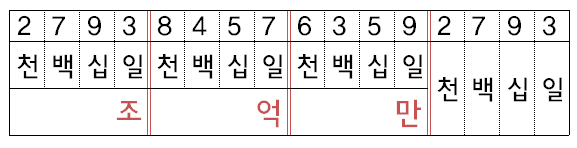
시간복잡도의 유형

• 빅오메가 : best case
• 빅세타 : average case
• 빅오(O(n)) : worwt case의 연산횟수. 항상 최악의 경우를 고려함

보통 n^2, nlogn 중 고민하게 된다

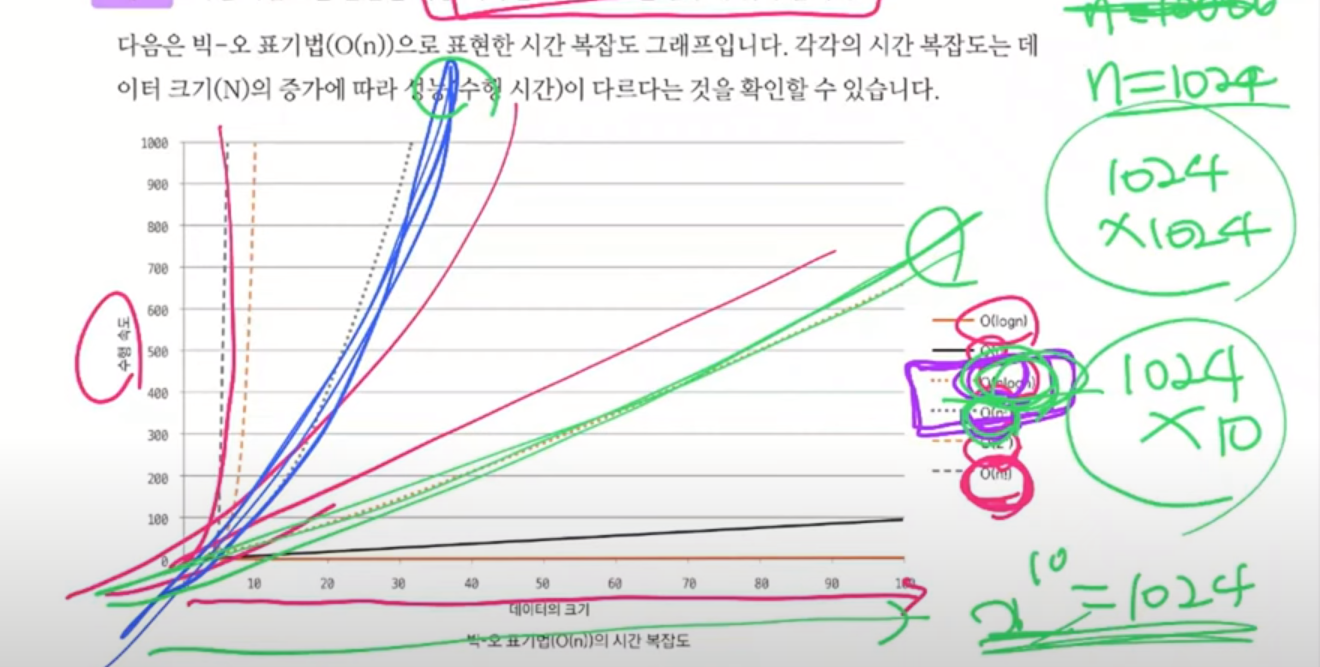
처리할 데이터가 많아질수록 차이가 급격하게 벌어짐

만약 시간제한이 2초인 경우

→ 2억번 이하의 연산을 해야되는구나! 도출하기

백만개의 데이터를 2초 안에 정렬해야하는 경우, 버블정렬(n^2) vs 병합정렬(nlogn)중에는 당연히 후자를 골라야함
why? nlogn 백만 -> 2천만번 < 2억번

알고리즘 잘 고른 것 같은데 시간초과가 나는 경우

가장 많이 중첩된 반복문의 시간복잡도를 살펴볼것!! (상수는 무시)

디버깅

• 디버깅 : 프로그램에서 발생하는 문법 오류, 논리 오류를 바로잡는 과정

음수가 나올 수 없는데 음수가 나왔다?

→ 자료형 체크!!! (overflow 발생했을 가능성 큼)
ex. int -> long long으로 바꿔보자

배열, 리스트, 벡터

배열의 특징

1. 인덱스를 사용하여 값에 바로 접근 가능
2. 새로운 값 삽입 / 특정 인덱스 삭제가 어려움 → 해당 인덱스 주변의 값을 이동시키는 과정 필요
3. 배열의 크기는 선언할때 지정, 한번 선언시 크기 변경 불가능
4. 구조가 간단하여 코테에서 많이 사용

리스트의 특징

(값, 포인터) 노드라는 것을 포인터로 연결한 자료구조

1. 인덱스가 없어서 Head 포인터부터 순서대로 접근. 접근 속도 느림
2. 포인터로 연결되어 있어 삽입/삭제 연산 빠름
3. 선언 시 크기 별도 지정할 필요 없음 (따로 크기가 정해져있지 X)
4. 포인터를 저장할 공간이 필요하여 배열보다 구조 복잡

벡터의 특징 (중요!)

C++ 표준 라이브러리에 있는 자료구조 컨테이너 중 하나
배열의 특징을 가지면서 배열의 단점을 보완한 동적 배열의 형태

1. 동적으로 원소를 추가할 수 있다. 크기가 자동으로 늘어남
2. 맨 마지막 데이터 삽입/삭제는 문제X. 중간 데이터의 삽입 삭제는 배열과 같은 매커니즘
3. 인덱스를 시용하여 접근 가능

#include <vector> 해줘야 사용 가능!

합배열

배열이 바뀌지 않을때, 구간합을 구하기 유용하다
배열 각 칸의 누적합을 저장해두고 특정 부분의 구간합을 구해야할 때 사용

배열 A
누적합 배열 S

S[i] = S[i-1] + A[i]

2~5 사이의 누적합 : S[5] - S[1]

만약 배열의 값이 자주 바뀐다면? -> 세그먼트 트리 (인덱스 트리) 사용

백준 1253 좋은 수 구하기

백준 1253. 버블소트

• 시간제한 2초
• 서로 다른 두 수의 합으로 특정 수를 만들어내야 하므로 좋은 수 판별 알고리즘이 N^2를 넘어가면 안된다. (하나하나 살펴보면서 처리해주면 안된단 뜻)

→ nlogn의 시간복잡도인 정렬 + 두 수를 체크해야 하므로 투 포인터 (O(N))

두 수를 살펴봐야 하는 경우 -> 투포인터를 의심하자

C++ 입출력 빠르게

int main(){
	ios::sync_with_stdio(false); 
    cin.tie(NULL);
    cin.tie(NULL);
}

• ios::sync_with_stdio(false); : C에서의 입출력 라이브러리 stdio, C++에서의 입출력 라이브러리 iostream의 버퍼 동기화를 분리. C++만의 버퍼를 사용해서 검사할 버퍼의 크기가 줄어들어 속도 향상
  (C언어 입출력함수 printf, scanf등 사용 불가)

• cin.tie(NULL); : cin, cout의 tie를 풀어준다. cin, cout은 기본적으로 tie되어있어 cin을 사용하기 전에 cout에서 출력할 값을 내보냄. 출력할 값을 버퍼에서 내보내는 flush 과정을 건너뛰므로 속도 향상
  (cout에서 입력을 받기 전에 무언가를 표시할 때마다 cin을 수동으로 플러시해줘야 함)

• endl 대신 \n 쓰기 : endl은 개행 후 버퍼를 비워주는 역할까지 하므로 단순 개행문자를 사용하는 것이 속도가 조금 더 빠르다

cin, getline 차이

• cin : 띄어쓰기(공백) 기준으로 입력받음. \n 만나면 저장하지 않고 버퍼에 넣어준뒤 그 전까지의 입력만 받음
• getline : 3번째 파라미터로 주어지는 것을 기준으로 입력을 분할하여 받음. 디폴트값은 \n. cin과 달리, \n 자체를 저장 가능

백준 1377 - 버블정렬

백준 1377. 버블소트
문제에서 시키는대로 버블정렬하면 시간초과난다. N은 50(510^5)만이므로 N^2를 하면 기준시간 2초(2억번 210^8)에 절대 못 들어온다.

따라서 버블정렬 내에서 최적화를 시켜주는 것이 아니라 문제에서 출력하는 값이 정확히 무엇인지를 판단하는 것이 중요하다

문제에서 출력하는 값 i는 몇 번의 swap이 일어났는지 그 횟수+1를 출력해주는 것이다. 즉, 반복문이 몇 번 돌았는지를 체크해주는 것!

핵심 아이디어는 정렬 후 인덱스 값 - 초기 인덱스값의 max값이 최대 반복 횟수와 같다는 것이다.

따라서 nlogn의 시간복잡도를 가지는 algorithm 라이브러리의 sort함수를 실행해준 뒤 인덱스값의 차이를 구해주면 된다.

(어렵다)

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N = 0;
	cin >> N;

	// (값, 인덱스) 쌍으로 넣어주기
	vector<pair<int, int>> A(N);

	for (int i = 0; i < N; i++) {
		cin >> A[i].first;
		A[i].second = i;
	}

	sort(A.begin(), A.end());

	int Max = 0;
	for (int i = 0; i < N; i++) {
		if (Max < A[i].second - i) {
			Max = A[i].second - i;
		}
	}

	cout << Max + 1;
	return 0;
}

정렬 여부를 처리해줄때 인덱스를 가지고 몇번의 swap이 일어났는지 체크해줄 수 있음을 알고가자!