오늘 푼 문제
누적합
누적합은 구간의 변화를 효율적으로 처리할 수 있는 방법이다. 누적합 개념 자체는 간단하다. 말 그대로 어떤 배열이 있을 때, 해당 인덱스까지의 합을 구하는 것이다.
만약 [1,2,3,4,5]라는 배열이 존재한다면, 누적합 배열은 [1,3,6,10,15]이 된다.
누적합은 특정 구간의 합을 구해야할 때 시간복잡도의 이점이 크다. 한번만 전체 배열에 대한 누적합을 계산해준다면, a번째 요소에서 b번째 요소까지의 합은 누적합 배열에서 (b번째까지의 합) - (a-1번째까지의 합)으로 나타낼 수 있다.
누적합을 활용할 수 있는 좋은 시나리오는 바로 연속되는 구간에 일정한 값을 더하거나 빼고 싶을 때이다. 매번 배열에 접근해서 직접 계산하는 것이 아니라, 누적합 배열을 사용하는 것이다.
만약 1차원 배열의 a번째 원소부터 b번째 원소까지 c만큼의 변화를 주겠다고 하면 새로운 배열의 a번째 원소에 c를 더하고 b+1번째 원소에 c를 빼면 된다.
(보다 자세한 설명은 아래 파괴되지 않은 건물을 참고하자)
Lv 3. 파괴되지 않은 건물 (해설참고)
Brute Force로 풀면 효율성에서 박살나는 문제다. (시간복잡도 O(N*M))
따라서 구간의 변화를 효율적으로 처리할 수 있는 방법 (누적합)을 사용해야 하는 문제다.
와 2022 카카오 공채 기출이던데 레벨 3정도의 난이도로 잡혀있다. 누적합 개념만 떠올리면 바로 풀 수 있어서 레벨 3인걸까. 그 당시에 이 문제를 본 사람들은 단번에 누적합 문제인걸 캐치한 사람만 효율성을 통과했겠지? 아직도 배울 것이 산더미다.
카카오 테크 블로그에 해설이 잘 나와있어서 보고 열심히 공부했다.
1차원 배열
예를 들어, [1,2,4,8,9]의 배열이 있고, 0번째부터 3번째 원소까지 2만큼 빼야 하는 상황이라고 가정한다. 즉, 배열을 [-1,0,2,6,9]로 만들고 싶은 상황이다. 가장 쉬운 방법으로는 0번째부터 3번째 원소까지 반복문을 사용해 2만큼 빼주는 방법이 있지만, 이 방법은 O(M)의 시간 복잡도가 걸린다.
O(M)의 시간 복잡도를 O(1)로 만들 수 있는 방법은 바로 누적합을 이용하는 방법이다. 위의 예시의 경우 [-2,0,0,0,2]를 저장한 새로운 배열을 생성한다. 이 배열을 앞에서부터 누적합하면 [-2,-2,-2,-2,0]이 되기 때문에 초기 배열인 [1,2,4,8,9]과 더해주면 [-1,0,2,6,9]를 얻을 수 있게 된다.
즉, 1차원 배열의 a번째 원소부터 b번째 원소까지 c만큼의 변화를 주겠다고 하면 새로운 배열의 a번째 원소에 c를 더하고 b+1번째 원소에 c를 빼면 된다.
이 방식으로 문제를 풀면 O(N * M * K)의 복잡도를 O(N * K)로 줄일 수 있지만, 이 또한 시간 초과가 발생한다. 따라서 이 아이디어를 2차원 배열로 확장해 줘야 한다.
2차원 배열로 확장하기
2차원 배열에서 (x1,y1)부터 (x2,y2)까지 n만큼의 변화는
(x1,y1)에+n(x1,y2+1)에-n(x2+1,y1)에-n(x2+1,y2+1)에+n
을 한 것과 같다. 위 배열을 위에서 아래로 누적합한 뒤, 왼쪽에서 오른쪽으로 누적합하거나 왼쪽에서 오른쪽으로 누적합 한 뒤, 위에서 아래로 누적합하면 처음에 의도한 (x1,y1)부터 (x2,y2)까지 n만큼 변화시키는 배열이 나오는 것을 확인할 수 있다.
누적합 처리
먼저 위에서부터 아래로 누적합을 계산해주고, 다음에 왼쪽에서부터 오른쪽으로 누적합을 처리해주면 된다.
최종 답안
누적합 배열과 원본 배열을 더한 뒤, 그 값이 0보다 큰 경우에는 파괴되지 않은 건물이므로 그 경우를 세주면 된다.
코드
def calcul(arr, r1, c1, r2, c2, degree):
arr[r1][c1] += degree
arr[r1][c2+1] -= degree
arr[r2+1][c1] -= degree
arr[r2+1][c2+1] += degree
def solution(board, skill):
answer = 0
arr = [[0 for _ in range(len(board[0])+1)] for _ in range(len(board)+1)]
for s in skill:
t, r1, c1, r2, c2, degree = s
# attack
if t == 1:
calcul(arr, r1, c1, r2, c2, -degree)
# defense
else:
calcul(arr, r1, c1, r2, c2, degree)
# 누적합 계산용 배열
acc_arr = [[0 for _ in range(len(board[0])+1)] for _ in range(len(board)+1)]
# 위에서부터 아래로 누적합
for r in range(len(arr)):
for c in range(len(arr[0])):
if r==0:
acc_arr[r][c] = arr[r][c]
else:
acc_arr[r][c] = arr[r][c] + acc_arr[r-1][c]
# 왼쪽에서부터 오른쪽으로 누적합
for r in range(len(arr)):
for c in range(len(arr[0])):
if c==0:
# 주의. arr[r][c]를 보면 안되고 누적합 배열을 봐야함
acc_arr[r][c] = acc_arr[r][c]
else:
acc_arr[r][c] = acc_arr[r][c] + acc_arr[r][c-1]
for r in range(len(board)):
for c in range(len(board[0])):
result = board[r][c] + acc_arr[r][c]
# 파괴되지 않은 건물일때 (내구도가 0보다 큰 경우)
if result > 0:
answer += 1
return answer실버 2. 백준 20438 출석 체크
출석코드를 받은 학생은 해당 학생의 입장번호부터 그 배수를 쭉 출석처리해준다. 만약 학생이 졸았다면 출석처리가 되지 않는다.
출석 테이블을 만들어서 풀어주면 되는 문제다.
다만 매번 범위 안에 몇개의 1이 있는지 세다간 시간 초과가 나는 문제.
따라서 누적합을 사용하여 해당 범위 안에 몇명의 학생이 미출석 상태인지를 계산해주는 방식을 사용해야 한다.
미출석 상태를 1로 처리, 출석 상태를 0으로 처리하여 구간 내의 1의 개수가 미출석된 학생의 수다. 따라서 누적합 배열acc을 계산해준 뒤, 시작범위 s, 끝 범위 e 내의 미출석 학생의 수를 구할 때는 간단하게 acc[e] - acc[s - 1] 값을 출력해주면 된다.
from sys import stdin
input = stdin.readline
# 학생의 수 N, 졸고 있는 학생의 수 K, 지환이가 출석 코드를 보낼 학생의 수 Q, 주어질 구간의 수 M
N, K, Q, M = map(int, input().split(" "))
# 졸고 있는 학생 번호
sleeping = list(map(int, input().split(" ")))
# 출석 코드를 받을 학생 번호
attend = list(map(int, input().split(" ")))
# 계산해야줘야 하는 구간 M개 받기
check = []
for _ in range(M):
check.append(list(map(int, input().split(" "))))
arr = [1 for _ in range(N + 3)] # 3 ~ N+2번째까지 사용, 1은 미출석
for a in attend:
if a in sleeping:
continue
# 더 작은 배수를 훑어본 상태이므로 계산해줄 필요X
if arr[a] == 0:
continue
# 출석 처리
for i in range(a, N + 3, a):
arr[i] = 0
# 조는 학생은 졸았으므로 미출석 처리
for s in sleeping:
arr[s] = 1
# 누적합 계산
acc = [0 for _ in range(N + 3)]
for i in range(N + 3):
if i == 0:
acc[i] = arr[i]
else:
acc[i] = arr[i] + acc[i - 1]
for s, e in check:
print(acc[e] - acc[s - 1])실버 1. 백준 11660 구간 합 구하기 5
정석 누적합 문제. 2차원 배열을 입력받고, 2차원 배열의 특정 범위 내의 누적합을 M번 출력해줘야 하는 문제다.
참고 블로그 이 분 블로그가 아주 좋아서 이해에 크게 도움이 되었다.
2차원 누적합
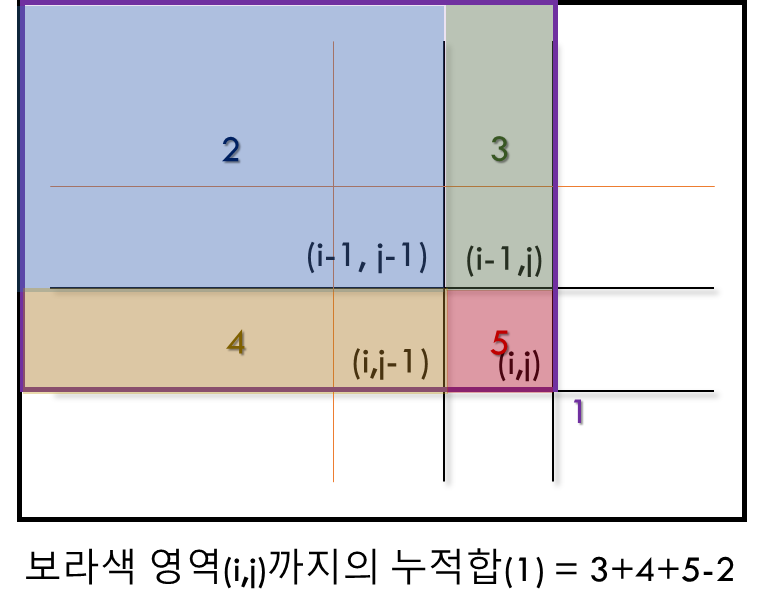
점화식을 원활하게 사용하기 위해 누적합 배열의 i=0, j=0의 데이터는 0으로 넣어 한칸씩 큰 배열을 만들어주었다. 따라서 누적합 배열의 인덱스는 실제 배열의 인덱스보다 1씩 크다는 것에 유의해야 한다.
2차원 부분합
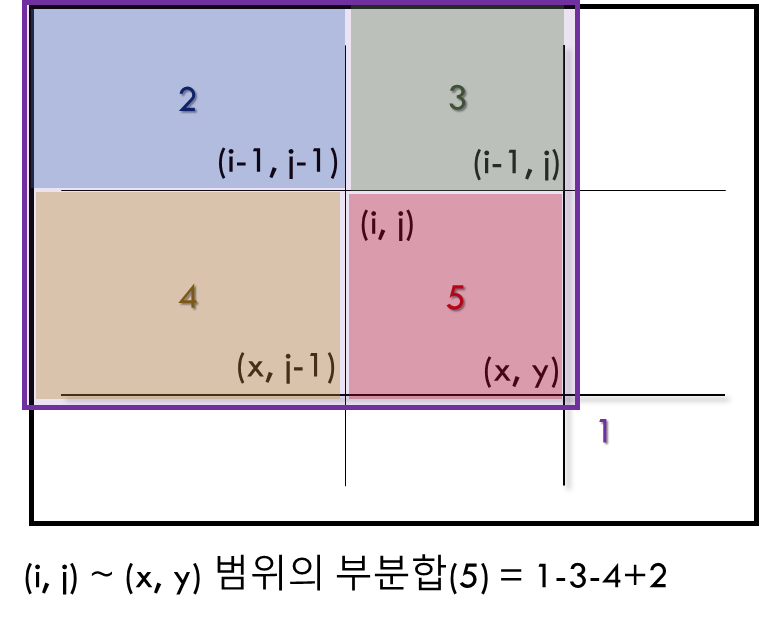
2번 영역이 두번 제외되기 때문에 한번 더해줘야 한다.
위의 해설에 기반하여 코드를 작성하면 다음과 같다.
from sys import stdin
input = stdin.readline
N, M = map(int, input().split(" "))
table = [list(map(int, input().split(" "))) for _ in range(N)]
pos_arr = [list(map(int, input().split(" "))) for _ in range(M)]
# 누적합 구하기
# 점화식을 원활하게 구하기 위해 i==0, j==0일때는 0으로 채운다
# 누적합 배열의 인덱스는 원본 배열보다 1씩 크다
acc = [[0 for _ in range(len(table[0]) + 1)] for _ in range(N + 1)]
# 누적합 배열 계산
for i in range(1, len(table) + 1):
for j in range(1, len(table[0]) + 1):
acc[i][j] = (
acc[i - 1][j] + acc[i][j - 1] - acc[i - 1][j - 1] + table[i - 1][j - 1]
)
# 문제에서 요구하는 데이터 출력하기
# 범위 내 부분합을 구하기
for i, j, x, y in pos_arr:
result = acc[x][y] - acc[i - 1][y] - acc[x][j - 1] + acc[i - 1][j - 1]
print(result)