[백준-자바] N_11726 2xn 타일링

0woy·2024년 10월 31일

DP 백준 자바 피보나치

코딩테스트

목록 보기

33/39

📜 문제

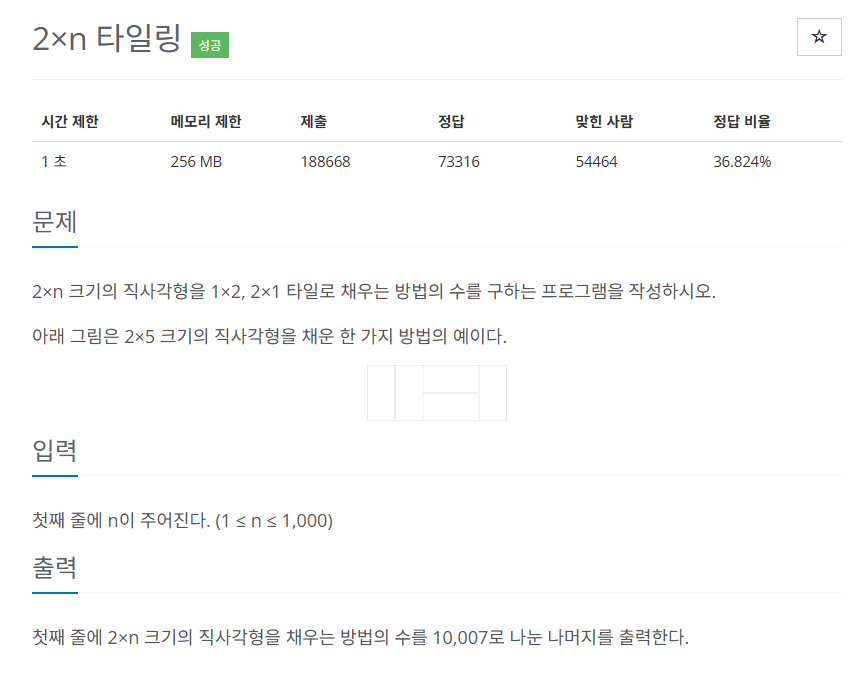
세로 길이가 2로 고정된 타일에 가로 길이 n이 주어지면,
2x1 (이하 세로 타일), 1x2 (이하 가로 타일) 타일로 채우는 방법의 수 구하기.

예전에 얘랑 씨름하다가 결국 답 봤던 것 같은데 마법처럼 어떻게 풀었는지 기억이 안 나서 새마음 새출발했다.

생각하기

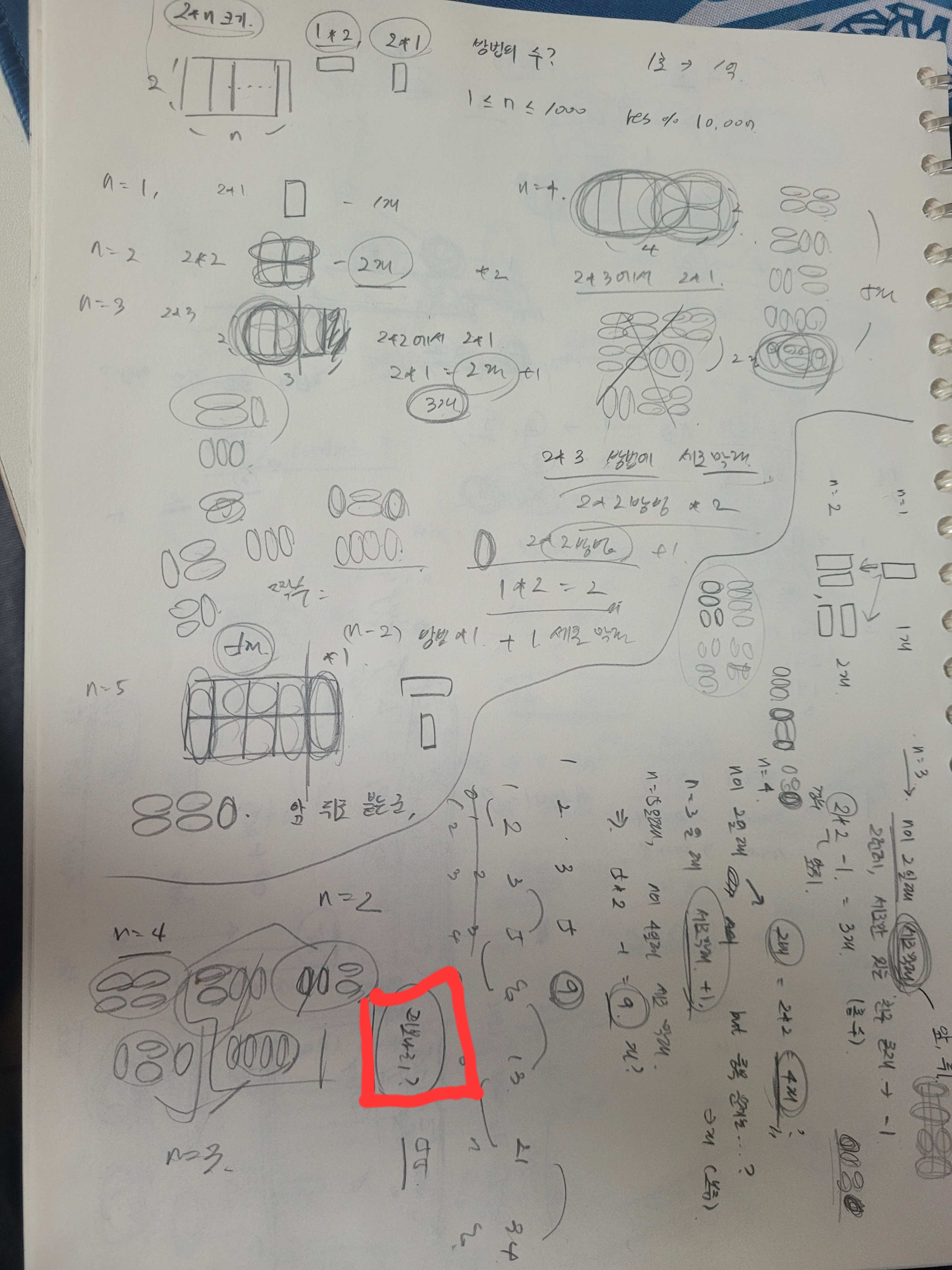
규칙을 찾기 위해 끄적인 노트를 가져왔다..

파블로프의 개처럼 경우의수 = dp 라고 떠올리게 돼서 냅다 규칙을 찾았다.
규칙이 보일랑 말랑하지만 딱 떨어지지 않아서 예제를 쳐다봤는데 익숙한 숫자 55가 보였다.
맞다. 이 숫자는 피보나치 수열에서 10번째로 오는 수다.

그래서 피보나치로 풀었음.

그치만, 예제를 보고 힌트를 얻어서 풀었기에 이렇게 넘어가면 안 된다.

접근 방식

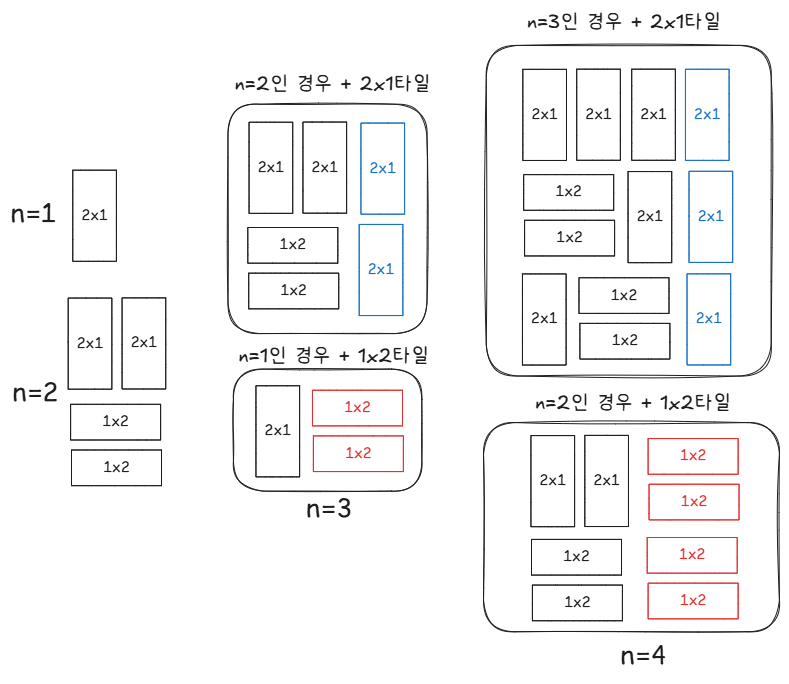
n이 3인 경우, (2x3)타일링을 하는 경우의 수는 위 그림에 나와있다.
자세히 보니 2x2 타일링에서 세로타일을 오른쪽에 붙이고, 2x1 타일링에서 가로 타일을 갖다 붙인 모양새다.

그렇다면, 가로 길이가 n인 타일링의 방법의 수 = n-1 타일링 방법 + n-2 타일링 방법임을 알 수 있겠다.

나는 처음 규칙을 찾을 때 n-2 타일링 방법을 이용하는 게 어려웠다.
왜냐하면 n-2타일링에서 세로타일 2개를 붙여서 n 타일링을 만들 수 있는데,
그렇게 하면 n-1 타일링에서 세로타일을 붙인 경우와 중복되는 부분이 있었기 때문이다.

다시 생각해 보니, n-2에서 세로타일을 붙인 경우는 n-1에서 세로타일을 붙인 경우에 모두 존재하기 때문에 신경쓸 필요가 없겠다.

세로 지옥에서 빨리 벗어났다면 피보나치 힌트를 보지 않고 풀 수 있지 않았을까 싶다.

🍳 전체 소스 코드

package DP;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class N_11726 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int [] dp = new int[n+2];
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++){
            dp[i]=dp[i-2]%10007+dp[i-1]%10007;
        }
        System.out.println(dp[n]);
    }
}