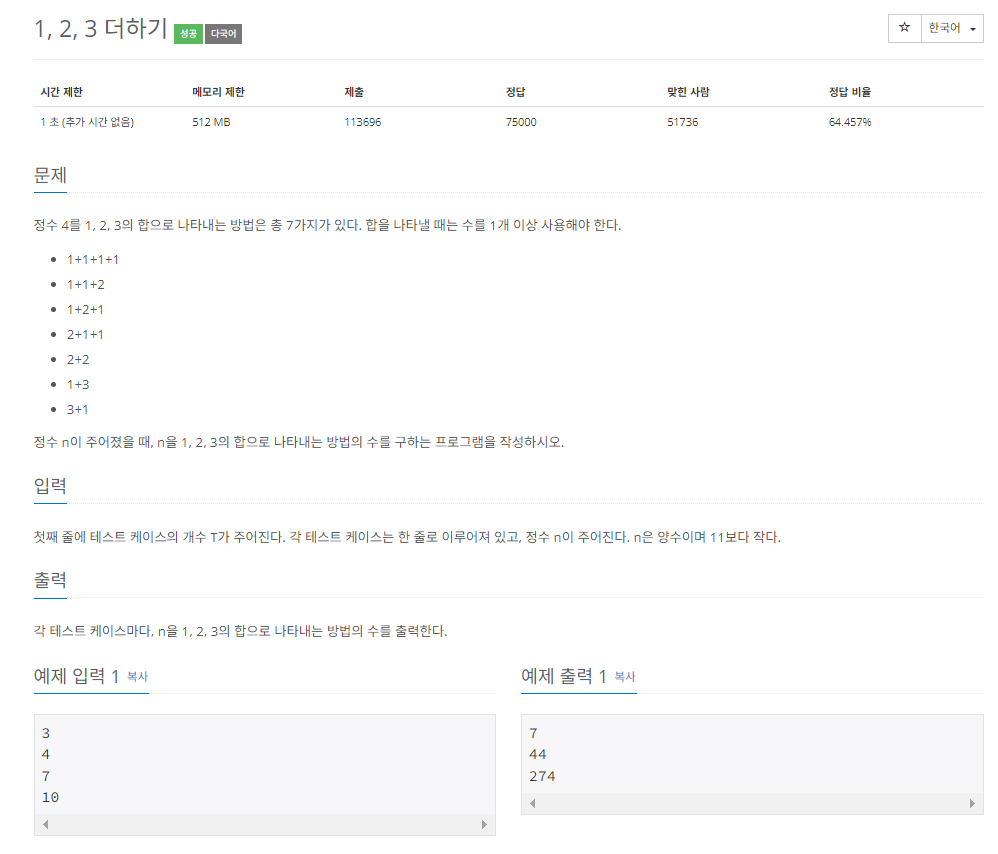
📜 문제
- 입력 받은 수를 1, 2, 3을 조합한 합으로 나타내는 가짓수를 구한다.
위 문제는 DP로 풀 수있다.
하지만, 처음 봤을때 순열 또는 조합 관련 문제인줄 알았다. . .
우선, 고정된 수인 1, 2, 3을 1, 2, 3을 조합한 합으로 나타내는 방법을 구하면
| 고정수 | 조합 | 가짓수 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1+1, 2 | 2 |
| 3 | 1+1+1, 1+2, 2+1, 3 | 4 |
위와 같이 나타낼 수 있다.
4의 경우 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 3+1, 1+3, 2+2로 총 7가지 경우다.
1+1+1+1,1+2+1,2+1+1,3+1은 고정수 3을 나타내는 조합에서 +1을 더한 결과값과 같다.
1+1+2와2+2는 고정수 2의 조합에서 +2를 더한 값과 같다.
1+3의 경우는 고정수 1을 나타내는 조합에서 +3을 더한 값과 같다.
즉, 4의 가짓수는 1, 2, 3을 1, 2, 3의 조합으로 나타낼 수 있는 가지수의 합과 같다. (4+2+1 =7)
5의 경우도 마찬가지다. 4의 조합에서 +1한 값, 3의 조합에서 +2한 값, 2의 조합에서 +3한 값이 5가 되므로 5의 가짓수 = 7+4+2 =13 이 된다.
따라서 점화식은 dp[n]=dp[n-1]+dp[n-2]+dp[n-3]가 된다.
✍ 부분 코드 설명
점화식을 이용해 N의 가짓수 구하기
for(int i=0;i<test.length;i++){
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
int n = test[i];
for(int j=4;j<=n;j++){
dp[j] = dp[j-1] +dp[j-2]+dp[j-3];
}
System.out.println(dp[n]);
}
dp 배열은 해당 인덱스의 가짓수를 저장한 배열이다.
입력 받은 n까지 반복하면서 n의 가짓수를 찾아가는 방식이다.
🍳 전체 소스 코드
package SWM;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class N_9095 {
public static void main(String [] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int count = Integer.parseInt(br.readLine());
int [] test = new int [count];
int [] dp = new int[12]; // n은 11이하의 정수
for(int i =0;i<count;i++){
test[i] = Integer.parseInt(br.readLine());
}
for(int i=0;i<test.length;i++){
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
int n = test[i];
for(int j=4;j<=n;j++){
dp[j] = dp[j-1] +dp[j-2]+dp[j-3];
}
System.out.println(dp[n]);
}
}
}✨ 결과
DP문제 너무 어렵다.
규칙을 찾으면 쉽게 풀 수 있는 문제인데 내 눈에만 규칙이 안 보이나보다.
다른 분들의 풀이를 보고 나서야 "헐 맞네"라는 생각이 드니까 말이다.
그치만 좌절하지 않지. DP 널 갖고 말테야.