[FP] 함수형 최적화

yongkini ·2024년 12월 25일
fpfunctional programminglodash take메모이제이션재귀함수최적화함수형함수형 최적화함수형 프로그래밍
1

Functional Programming

목록 보기
20/21

함수형 최적화

함수형 최적화?

: 함수형 프로그래밍을 하는데 있어서 여태까지 '최적화'라는 측면에서 살펴본적은 없다. FP를 할 때 데이터 흐름을 함수형 세계관으로 관리하기 위해서 모나드, 체이닝을 쓰고, 프로그램 로직 흐름을 컨트롤하기 위해서 합성을 이용하며 이를 표현하기 위한 툴들을 주로 알아봤다. 그리고, 함수형의 세계관을 OOP와 비교하면서 좀 더 잘 이해해보려고 했고, 전반적으로 함수형의 개념 그리고 그것을 이해하기 좋게 혹은 써먹기 좋은 툴들을 알아봤었다. 그러면 함수형에서 '최적화'라는건 뭘 의미할까?. 사실 함수형 프로그래밍을 배우면서 혹은 실제 프로젝트에 써먹으면서 비유적으로 표현해보면 "이게 만약 '코딩테스트'였고, 메모리나 속도 제한이 있는 문제였다면 내 코드는 최적의 코드는 아닌데" 라고 생각한적이 많았다. 정말 간단한 예시로 map, filter 등을 주로 쓰다보면 함수를 하나의 '값'으로 생각하는 FP식 사고로 가독성 좋은 심플한 코드가 되는 것은 아주 만족스러웠으나, 굳이 여러번 로직을 돌리게 되는 상황들이 꽤나 자주 생겼다. 

const mapAndFilteredArr = arr.map(age => age + 1).filter(age => age > 31);

예를 들어, 위의 데이터는 사람의 나이 데이터를 가져온 다음에 연말인 상황에 맞게 1살을 모두 + 해주고, 그 중에 내년에 31살이 넘는 사람들의 데이터를 표현한 것이다. 함수형 프로그래밍을 하는 데에 있어서 위의 코드는 큰 문제가 없다. 너무 직관적이고 심플하게 값을 표현했기 때문이다. 하지만, 저 코드를 '최적화' 해보면 이렇게 할수도 있다.

const ageArr = [ ... ];
const mapAndFilteredArr = [];
ageArr.forEach(age => {
	if(age + 1 > 31) {
    	mapAndFilteredArr.push(age + 1);
    }
});

위와 같이 해주면 만약에 ageArr가 10000개의 데이터를 갖고 있는 배열일 때, 10000번의 시행만 해주면 된다. 하지만, 이전 코드는 10000 + 10000번의 시행을 하게된다. 물론 그래봤자 O(N) 이지만, 극도의 효율성과 최적화를 생각하는 사람에게는 꽤나 예민한 주제일 수 있고, 10만개의 데이터라고 하면 N+N = O(N) 이라도 무시못할 수준의 비효율성이 초래된다.

앞서 본 예시처럼 함수형에서 비효율적인건 저런걸 의미한다(물론 다른 것도 있고 그 부분도 다룰 것). 그럼 함수형 최적화는 저러한 함수형 프로그래밍을 지향해서 생긴일(?)을 최적화 하는 것으로 이해하면 된다.

함수형 최적화 종류

느긋한 평가로 실행 늦추기

: 여기서도 예를 들어서, 생각을 해보자. 만약에 upbit OpenAPI를 통해서 코인 데이터를 가져오는데, 코인 리스트의 각 코인 정보에는 가격, RSI를 구할 수 있는 메타 정보들, 시가총액 순위 정보가 들어있다고 해보자.

RSI 값이 70 이상이면 과매수 상태, 30 이하이면 과매도 상태로 본다

이 정보들을 바탕으로 RSI값을 구하고, RSI값을 통해서 과매도 상태인 코인을 필터링하고, 마지막으로 시가총액 50위 안에 드는 코인으로 한정하여 이 조건을 만족하는 5개의 코인을 같은 비율로 분할매수하는 자동 매매 프로그램을 만든다고 해보자.

그럼 대략 이렇게 될 것이다.

const response = await getMetaDataAPI(); 
const coinList = response.data.map(getRSIWithData)
							  .filter(RSIIsUnder30)
                              .filter(RankIsUnder50)
                              .slice(0, 5);

보통의 경우에는 사실 이렇게 해도 큰 문제가 없다고 판단한다. 하지만, 여기서 중요한건 5개의 코인만 걸러내면 된다는 것이다. 예를 들어, 처음 API를 가져왔을 때 데이터의 개수는 엄청 많을 것이다(뭐.. 어떻게 가져오냐에 따라 다르겠지만, 전체 코인을 다가져올 수 없어서 일부만 가져온다쳐도 그 양은 엄청나다). 이 때, RSI를 구하는 로직이 굉장히 복잡한 연산이라고 가정해보면, 그 많은 데이터에 대해서 getRSIWithData 계산을 모두 시행해야한다(정작 필요한 데이터의 개수는 5개인데 말이다). 이런 경우에 lodash의 chain, value, take를 활용하면 최적화를 할 수 있다(물론, 최적화가 되지 않을 수 있다?).

import _ from "lodash"

const response = await getMetaDataAPI(); 
const coinList = _.chain(response.data).map(getRSIWithData)
							  .filter(RSIIsUnder30)
                              .filter(RankIsUnder50)
                              .take(5)
                              .value();

이렇게 해주면 된다.

이렇게하면 본래는 response.data의 모든 데이터에 대해 map을 쭉 실행하고(getRSIWithData 함수를 모든 데이터에 적용하고), filter 로직을 거쳐 결과를 리턴하는 플로우로 진행될 coinList가 response.data 배열의 첫번째 요소를 기준으로 

|   getRSIWithData
|   RSIIsUnder30
|   RankIsUnder50
V

이런식으로 요소 하나에 대해서 getRSIWithData, RSIIsUnder30, RankIsUnder50를 모두 실행하고, 다음 요소로 넘어가는 식의 플로우로 진행된다.

무슨 말인가하면,

[BTCData, ETHData, DogeData, LinkData, DotData, SHIBData, .... ]

이렇게 데이터가 있을 때 본래 로직이었으면(최적화 X),
일단 map을 실행하고,

[getRSIWithData(BTCData), getRSIWithData(ETHData), getRSIWithData(DogeData), getRSIWithData(LinkData), getRSIWithData(DotData), getRSIWithData(SHIBData), .... ]

그 다음에 RSIIsUnder30 로직을 실행해 실제로 필터링을 하고, 모든 데이터에 대해 필터링을 1차적으로 했으면, 이번엔 RankIsUnder50 로직으로 필터링하고, 이런식으로 진행한 다음에 최종적으로 앞에서 5개를 slice할 것이다. 하지만, 최적화를 하면

1) getRSIWithData(BTCData)
2) RSIIsUnder30 에 필터링 되는가 체크
3) RankIsUnder50 에 필터링 되는가 체크
4) 필터링에서 살아남았으면 take(5) 부분에 의해 최종 결과물에 ++ 

1) getRSIWithData(DogeData)
2) RSIIsUnder30 에 필터링 되는가 체크
3) RankIsUnder50 에 필터링 되는가 체크
4) 필터링에서 살아남았으면 take(5) 부분에 의해 최종 결과물에 ++ 

// <<< 현재까지 최종 결과물에 벌써 2개의 데이터가 쌓였다고 해보자. >>> 
... processing..
...

43번째 데이터 진행 중 
1) getRSIWithData(SandData)
2) RSIIsUnder30 에 필터링 되는가 체크
3) RankIsUnder50 에 필터링 되는가 체크
4) 필터링에서 살아남았으면 take(5) 부분에 의해 최종 결과물에 ++

이 때 43번째 데이터 진행 중에 최종 결과물에 목표치인 5개가 채워졌다고 해보자. 최적화를 한 방식이라면, 더이상 로직을 진행하지 않는다. 따라서 API에서 return 받은 배열의 length - 43개의 데이터에 대해서는 더이상 RSI를 구할 필요도 없고, 애초에 더이상 로직을 진행할 필요없이 5개의 코인 데이터를 배열에 넣어서 로직을 끝낸다(= 필요한 것까지만 계산한다 === 필요할 때까지 계산하지 않는다).

이 최적화는 딱 이런 상황에 쓰기 좋다. 개수가 정해져있고, 조건이 명확해서 이미 원하는 목표치의 개수를 채웠다면 뒤의 데이터에 대해서는 계산할 필요가 없는 로직의 최적화에 적합하다. 물론 chain, value(lodash)를 쓰면 그 자체가 '지연 평가'의 혜택을 준다. 바로 실행하는게 아니라 말그대로 평가를 지연시키기 때문이다. 하지만, 중간에 필요없다고 판단되는 부분에 대해 평가 중단을 하는 최적화는 방금 말한 것처럼 take와 같이 쓰는 부분에서의 최적화가 해당된다.

rxjs와 비교를 해보면, lodash 같은 경우 take를 써야지만, rxjs와 같이 generator 방식으로 실행되는 최적화의 이점을 누릴 수 있다. 

const { map, filter, tap, take } = rxjs.operators
const { of } = rxjs

of(1, 2, 3, 4, 5, 6)
  .pipe(
    map(x => x + 1),
    tap(x => console.log(x)), // 로그 출력
    filter(x => x % 2 === 0),
    take(3)
  )
  .subscribe(x => console.log('Final result:', x));

위의 코드는 rxjs로 1~6까지 자연수에 +1을 해주고, 그중에 짝수만을 Final result로 출력하는 로직이다. 중간에 tap을 둬서 콘솔을 찍도록 해봤다(어떤식으로 처리되는지를 보기 위해). 그리고 그중에 앞에서부터 3개만 take로 가져오도록 했다.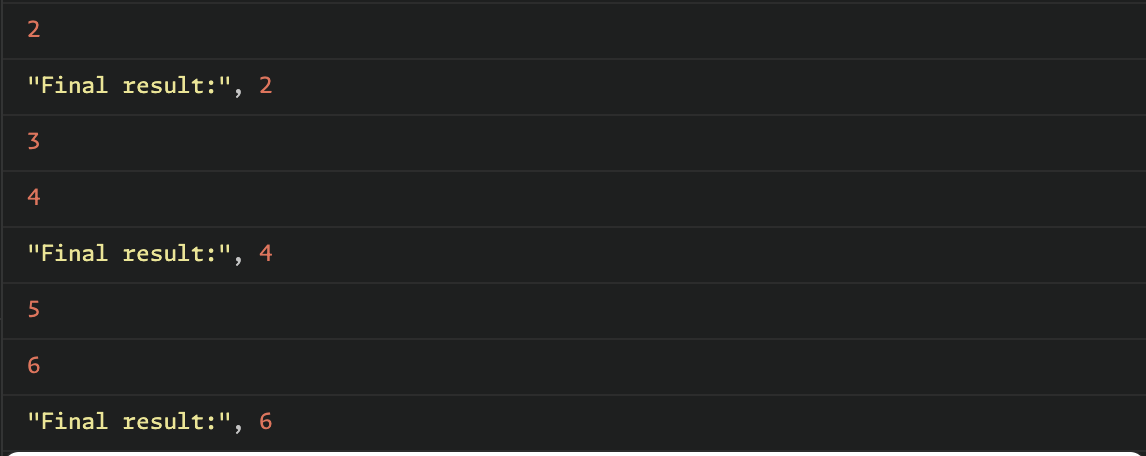

결과를 보면, 1,2,3,4,5,6 -> 2,3,4,5,6,7 총 6개의 숫자중에 콘솔을 거친건 2,3,4,5,6이다. 즉, 마지막 데이터인 7을 체크하기 전에 take(3)으로 인해 7은 체크를 하지 않았다. 여기까지는 lodash에서 chain, take를 쓴 것과 동일하다. 하지만, rxjs 같은 경우에는 take를 쓰지 않아도, generator 를 쓰는 것처럼 배열의 요소를 앞에서부터 한개씩 로직을 적용한다. 

const { map, filter, tap, take } = rxjs.operators
const { of } = rxjs

of(1, 2, 3, 4, 5, 6)
  .pipe(
    map(x => x + 1),
    tap(x => console.log(x)), // 로그 출력
    filter(x => x % 2 === 0)
  )
  .subscribe(x => console.log('Final result:', x));

무슨 말인가 하면 이번에는 take를 빼고 실행해보자.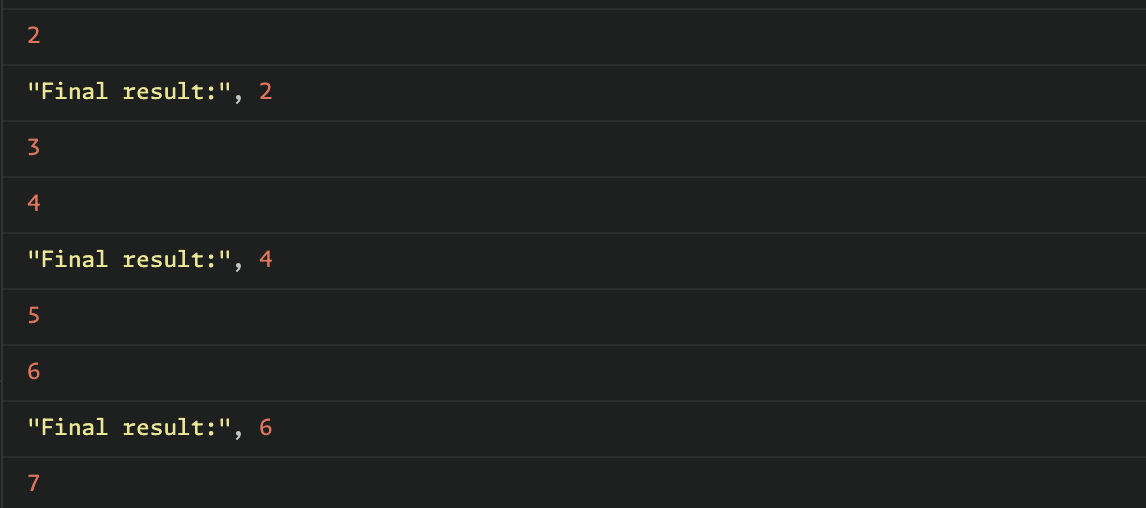위와 같이 콘솔창에 출력된다. lodash는 take를 쓰지 않는 이상 chain에 담긴 모든 배열에 대해서 map을 실행하고, 그 다음에 그 mapped 배열에 filter를 적용한다. 하지만 rxjs 같은 경우에는 애초에 배열에 operator로 로직을 적용할 때 콘솔창에 출력된 것처럼 요소 하나하나에 대해 순차적으로 실행한다. 그리고 구독자에게도 순차적으로 전달돼 저런식으로 Final Result가 앞에서부터 하나하나 출력된다.

메모이제이션(a.k.a '필요할 때 부르리' 전략?)

: 함수형 프로그래밍과 캐싱 및 메모이제이션 로직은 합이 잘맞는다. 그 이유는 FP는 '순수함수'를 지향하기 때문이다.

순수함수에서의 포인트는 '부수효과'가 없다는 것이다. 또한, 함수형의 특징 중 하나인 '참조 투명성'이 지켜진다. 즉, 부수효과가 없기 때문에 참조 투명한(= 같은 파라미터를 넣어주면 무.조.건 같은 결과가 나온다) 함수가 되는 것이다. 이런 특징을 가진 함수형 프로그래밍의 순수함수들은 메모이제이션을 적용하기 적합하다. 그 이유는 부수효과가 있는 순수하지 않은 함수에서는 같은 파라미터를 넣어도 다른 결과가 나올 수 있기 때문에 이를 캐싱해서 쓰게되면 잘못된 결과를 도출할 수 있다. 혹은 원하지 않은 플로우로 프로그램에 오류가 생길 수 있다. 그럼 메모이제이션 최적화는 어떤걸 의미하며, 어떻게 하면 될까?

const memoize = (fn) => {
  const cache = new Map();

  return function (...args) {
    const key = JSON.stringify(args);
    if (cache.has(key)) {
      return cache.get(key);
    }
    const result = fn.apply(this, args);
    cache.set(key, result);
    return result;
  };
}

나는 일단 위의 함수를 이용해서 해볼 계획이다. 간단하게 설명해보면, 위 함수에 특정 함수를 넣어주면, 그 함수를 실행할 때 예를 들어, A를 넣어서 한번 실행을 한 다음에, 그 다음에 우연히? 혹은 어쩌다보니 A가 또 파라미터로 들어온 경우에는 내부 로직을 거치지 않고, 캐싱해놓은(Map에) 값을 리턴해주기만 하는 식으로 최적화를 한다. 리액트의 useMemo 를 생각해보면 dependencies에 state가 안바뀌면 이전의 값을 그대로 가져다 쓰는식으로 메모이제이션 최적화를 하는데, 여기서는 파라미터가 이전에 썼던(그 함수 기준) 파라미터라면 어차피 부수효과가 없는 순수함수라 무조건 결과값이 동일할 것이므로 캐싱해둔 값을 리턴하는 것이다.

앞서 리액트에서 useMemo 등의 최적화를 하더라도, FP의 메모이제이션은 여전희 유의미하다(사실 별개다). 리액트에선 state의 변동을 체크하는거고, FP의 메모이제이션은 state가 바뀌었어도(이전 state와 비교했을 때), 한참전에 이미 한번 로직을 돌린 state가 또 들어오는 경우 굳이 그 함수 로직을 또한번 실행하지 않도록 막을 수 있기 때문에, useMemo 최적화와는 별개로 쓸 수 있다. 하지만, 보통 React.memo 나 useMemo 모두 마찬가지로, 간단한 로직에는 굳이 메모이제이션 최적화를 하면 오히려 비용이 크고, 최적화의 이점은 별로 누리지 못할 수 있는 것처럼 이러한 함수형의 메모이제이션도 적용시에 충분한 고려가 필요할 것 같다.

이러한 메모이제이션 최적화는 함수형의 꽃(?)인 재귀함수의 함수에도 적용할 수 있다. 예를 들어, 

const factorial = memoize(
  (val) => val * (val - 1 === 0 ? 1 : factorial(val - 1))
);

const testFactorialSpeed1 = IO.from(start)
  .map(R.tap(() => console.log(factorial(2000))))
  .map(end);

const testFactorialSpeed2 = IO.from(start)
  .map(R.tap(() => console.log(factorial(2001))))
  .map(end);

console.log(`걸린 시간은 ${testFactorialSpeed1.run()} 입니다.`);
console.log(`걸린 시간은 ${testFactorialSpeed2.run()} 입니다.`);

위 코드는 2000 팩토리얼과 2001 팩토리얼을 계산하는 부분을 메모이제이션 최적화를 통해 테스트를 해보는 로직이다.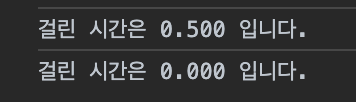
위의 콘솔 출력에 대한 결과물은 위와 같다.

즉, 2000 팩토리얼을 먼저 했을 때 0.5ms 가 걸렸으나, 그 다음에 2001 팩토리얼을 하니까 0.000ms가 걸린 것이다.

어떻게 이럴 수 있을까? 2001이 더 높은 숫자인데 적어도 2000 팩토리얼을 했을 때랑 같거나 조금더 많아야 정상 아닌가?.

이 결과는 메모이제이션 최적화로 가능했다. 재귀함수로 만든 팩토리얼 함수를 위에서 만든 memoize 함수로 감쌌다. 이에 따라 factorial(2000)을 한번 실행했으면 2000 팩토리얼에 대한 결과값이 caching map에 저장된다(스코프, 클로저 개념을 기억해보면 memoize안에 cache에 factorial이 어떻게 접근했는지 알 수 있다). 그에 따라 다음에 factorial(2001)을 호출하면 재귀로직에 따라 결국 2001 * factorial(2000)을 호출하게 된다. 즉, factorial(2000)을 다시 호출하게 된다. 이에 따라 바로 캐싱된 데이터에서 값이 리턴될 것이고 사실상 factorial(2001)은 연산을 거의 하지 않는다(실행 컨텍스트 스택이 2개 쌓이고 끝난다고 이해해도 된다).

이처럼 메모이제이션은 재귀함수의 최적화에도 도움을 준다(+ 커리로 만든 함수에 개별로 적용해도 됨).

PS. 생각해보면, 예를 들어, literally 객체(JS는 사실 모두 객체니까)를 파라미터로 넣을 때는 비교법을 달리할 필요가 있을수도 있겠다(혹은 이런건 최적화를 포기하던지). 예를 들어, 

const ab = {
  "a": 2, "b": 3
}

const ba = {
  "b": 3, "a": 2
}

위 두 데이터는 사실상 같은 데이커다. 하지만, stringify를 키로 캐싱하는 내 로직상으로는 두 데이터는 다른 데이터로 취급될 것이다. 이부분은 객체인 경우 키 설정하는 방법을 고치는 등 다른 전략을 쓰면 커버가 가능하다.

재귀함수 최적화 with TCO, Trampoline

: 본래 FP 전용 언어에서는 for loop 문법 자체가 없어서 '무조건' 재귀함수를 써야하는 경우도 있다고 한다. 하지만, JS 의 경우에는 그런건 아니라서 사실 재귀함수를 필수적으로 써야하는 것은 아니지만, 보통 보면 로직을 짤 때 재귀함수 식(?)으로 사고를 하면 더욱 심플한 경우가 있고, 이에 따라 재귀함수로 구현하는게 편한 경우가 있다(함수형식 사고라고 해보자). 하지만, JS 엔진의 로직을 뜯어보면, JS 공부할 때 자주보던 실행 컨텍스트 스택이 있을건데, 재귀함수는 러시아 인형처럼 하나의 함수를 실행하면, 그 안에 본인을 다시 호출하는 부분에서 실행 컨텍스트 스택 하나가 러시아 인형처럼 뿅? 하고 튀어나와 스택에 쌓이는 식이다. 개발 지식을 공유하는 플랫폼인 StackOverFLow 도 JS에서 Maximum stack count를 넘어서게 되면 볼 수 있는 에러의 이름이다. 이 때, for loop와 달리 재귀함수는 앞서 말한 것처럼 실행 컨텍스트 스택의 각각의 실행문을 쌓게 되고, 이는 결국 그만큼 메모리를 써야한다는 것을 의미한다. for loop 문을 쓰게되면 실행 컨텍스트 스택에 계속 쌓이는게 아니라 쌓이고, 실행하고 한번의 loop를 끝내면 pop되고 다음 loop가 다시 쌓이고 이런식이라 메모리 사용이 재귀함수에 비해 효율적이다. 그러면 재귀함수는 쓰면 안되는걸까?...

일단, 함수형 프로그래밍을 추구하는 사람들은 함수형 프로그래밍이 주는 '이점들', 예를 들어, 유지보수성, 가독성 등등을 가져가고(우선하고), 효율을 희생하는 것이 어쩔 수 없음을 인정한다. 혹은 그쪽을 더 지향한다. 사실 현대에 컴퓨터 성능상 우리가 작성한 코드들(FE 기준) 중 대부분은 수 밀리초 정도 빨라진다고 성능상 크게 달라질 것은 없다고 보는게 맞다.

어쨌든, 위의 관점으로 보더라도 최적화 방법은 알아보자.

TCO(Tail Call Optimization) = 꼬리물기 최적화

: TCO는 아까 factorial을 예로 들면(TCO 이거 사실 코딩테스트할 때, 결과값을 담는(?) 배열을 다음 재귀 함수 호출 파라미터에 넣어주면서 결과값을 모아갈 때 자주썼던 로직이다),

const factorial = (val) => val * (val - 1 === 0 ? 1 : factorial(val - 1))

이렇게 짰었는데, 이 로직을

const factorial = (n, current = 1) => (n === 1) ? current : factorial(n - 1, n * current);

이렇게 바꾸몀 비꼬리 호출 재귀함수를 꼬리호출 재귀함수로 최적화한 것이다(=TCO).

아까 실행 컨텍스트 스택을 가지고 이해해보면 TCO를 한 factorial은 사실상 for loop를 실행한 것과 마찬가지로, 한번의 로직을 실행하고, 다음 로직을 실행할 때 이전 실행 컨텍스트를 pop 하고 다시 쌓는 식으로 로직이 진행된다. 이전 실행 컨텍스트에서 다음 실행 컨텍스트가 나와서 계속 쌓이는 비꼬리 호출과는 이런 점에서 차이가 있고, for loop 에서는 스택 오버 플로우와 같은 문제가 생길 일이 없듯이, TCO가 제대로 이뤄지면 최적화를 할 수 있다. 하지만, 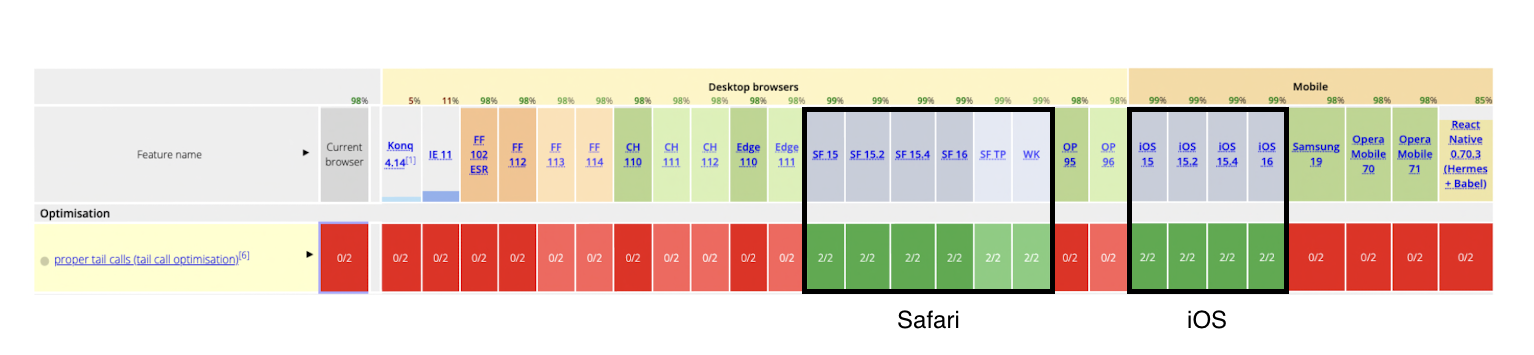현재 TCO 를 지원하는 엔진은 Webkit이 유일하다고 한다. 그래서 사실상 이걸 써먹기는 무리일 것 같다.

Trampoline

: 실제로 프로젝트를 진행할 때 재귀함수로 로직을 짠적이 있는데, 최적화를 해야하는 상황에 TCO가 안된다는 것을 고려했을 때 쓸 수 있는 방법이 뭐가 있을까 하여 써먹은 방법이다. 

export const trampoline = (fn: any) => {
  return function (...args: any) {
    let result = fn(...args);
    while (typeof result === "function") {
      result = result();
    }
    return result;
  };
};

내가 쓰는 모노레포에서 이런식으로 만들어놓고 쓰는데, 앞서 말했듯이 재귀함수를 쓰는 장점은 함수형 사고를 통해 로직을 더 심플하게 짤 수 있다는 것인데, JS내에서 이걸 쓰자니 최적화 문제가 생긴다. 그럼 trampoline은 뭐냐하면 재귀함수식 사고를 그대로 쓰게 냅두되 그 안에 돌아가는 로직만 for loop 처럼 돌도록, 즉, 실행 컨텍스트 스택 메모리 낭빌르 하지 않도록 하는 것이다. 일종의 눈속임(?)을 가능케 해주는 함수로 재귀함수를 래핑하는거다. trampoline을 쓰려면 꼬리 호출 최적화를 할 때처럼 함수를 만들어서 넣어주면 된다(비꼬리 호출 재귀함수처럼 만들어서 넣으면 제대로 동작하지 않는다).

마무리

함수형 최적화로 느긋한 평가, 메모이제이션, 재귀함수의 최적화를 알아보았다. 실질적으로 써먹기엔 메모이제이션 파트를 제일 많이 써먹지 않을까 싶다.

또한, 함수형을 할 때 최적화가 필요한 경우에는 써먹지만, 결국엔 함수형 프로그래밍을 위해 어느정도의 효율성보다는 함수형이 주는 이점을 가져가도 된다 혹은 그러한 방향을 지향해도 된다 라는 점이 뭔가 좀 혁신적(?)으로 나에게 느껴졌던 것 같다.

profile
yongkini
완벽함 보다는 최선의 결과를 위해 끊임없이 노력하는 개발자
이전 포스트

[FP] IO 모나드

다음 포스트

[FP] Promise 모나드

0개의 댓글