비교 정렬 알고리즘
지금까지 살펴본 정렬들(버블 정렬, 선택 정렬, 삽입 정렬, 합병 정렬, 퀵 정렬)은 모두 비교 정렬 알고리즘에 속한다.
- 공통적으로 주어진 시점에서
2개의 항목을 비교한다. - 평균 시간 복잡도가
O(n^2)~O(n log n)이다.
더 빠른 정렬 알고리즘이 있을까?
있다. 하지만 비교 정렬이 아닌 다른 방식으로 가능하다.
수학적으로 비교 정렬의 평균 시간 복잡도에는 하한선이 있기 때문이다.
비교 정렬 알고리즘이 아닌, 데이터의 특별한 속성을 이용한 정렬 방식이 있다.
=> 그것이 바로 기수 정렬(Radix sort)이다.
📌 기수 정렬(Radix Sort)
비교를 수행하지 않는 특별한 정렬 알고리즘.
- 숫자로 작동한다.
- 숫자 크기에 대한 정보를
자릿수로 인코딩 한다.
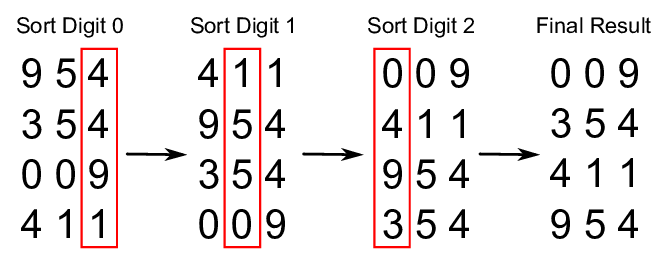
일의 자리수를 기준으로 오름차순으로 정렬
십의 자리수를 기준으로 오름차순으로 정렬
백의 자리수를 기준으로 오름차순으로 정렬
...
가장 큰 수의 자릿수가 끝날 때까지 반복하다 보면 정렬이 되어 있다.
기수 정렬의 helper function
1. getDigit(num,place)
: 수와 위치를 받아서 그 위치의 숫자를 반환하는 함수
ex. getDigit(12345, 0) -> 일의 자리수 숫자 반환 : 5
getDigit(12345, 1) -> 십의 자리수 숫자 반환 : 4
자릿수를 알아내는 방법은 10의 제곱수를 이용하는 것이다.
10의 0제곱 = 1 (일의 자리수)
10의 1제곱 = 10 (십의 자리수)
10의 제곱 = 100 (백의 자리수)
- 음수가 입력될 수도 있으므로 num에 절댓값을 씌워준다.
- 최대 자릿수를 넘으면 0이 출력된다.
구현
function getDigit(num, i){
return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}
// getDigit(12345, 1)
// 12345 / 10 = 1234.5
// 1234.5를 내림하여 1234
// 1234 % 10 = 4 (일의 자리수)2. digitCount(num)
: 자릿수 계산해주는 함수
ex. digitCount(2) -> 1
digitCount(25) -> 2
분류하는 시행을 몇 번 반복할지 알아내려면 가장 큰 수의 길이를 알아내야 한다.
ex. [4,7,29,408] -> 가장 큰 수인 408은 일의 자리, 십의 자리, 백의 자리를 모두 보아야 하므로 3번만큼 반복해야 한다.
Math.log10(num): 10을 몇 번 제곱해야 num이 나오는지 알려줌.- 나누어 떨어지지 않으므로 floor해주고 + 1
구현
function digitCount(num){
if(num === 0) return 1;
return Math.floor(Math.log10(Math.abs(num))) + 1;
}
// Math.log10(423) = 2.62634..
// 내림해서 2
// 2 + 1 = 3 (= 423의 길이)3. mostDigits(nums)
: 숫자들이 담긴 배열을 받아서 가장 큰 자릿수를 알려주는 함수.
(digitCount활용.)
ex. mostDigits([1234, 56, 7]) -> 4
Math.max()를 활용해서 기존 값보다 클 때만 갱신되도록.
function mostDigits(nums){
let maxDigits = 0;
for(let i=0;i<nums.length;i++){
maxDigits = Math.max(maxDigits, digitCount(nums[i]));
}
return maxDigits;
}기수 정렬 구현
// helper function
function getDigit(num, i) {
return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}
function digitCount(num) {
if (num === 0) return 1;
return Math.floor(Math.log10(Math.abs(num))) + 1;
}
function mostDigits(nums) {
let maxDigits = 0;
for (let i = 0; i < nums.length; i++) {
maxDigits = Math.max(maxDigits, digitCount(nums[i]));
}
return maxDigits;
}
function radixSort(nums){
let maxDigitCount = mostDigits(nums);
for(let k = 0; k < maxDigitCount; k++){
let digitBuckets = Array.from({length: 10}, () => []); // 배열 안에 10개의 하위 배열을 만들어줌.
for(let i = 0; i < nums.length; i++){
let digit = getDigit(nums[i],k);
digitBuckets[digit].push(nums[i]);
}
nums = [].concat(...digitBuckets);
}
return nums;
}
radixSort([23,345,5467,12,2345,9852])Spread Operator와 concat
spread operator로 이중 배열을 풀고 concat으로 합쳐줌.
[ ].concat(...[[[1],[2],[3]])
-> [1,2,3]
⭐️ 기수 정렬의 Big O
n = 배열의 길이 (= 정렬할 항목의 갯수), k = 항목의 자릿수
시간 복잡도 : O(nk)
공간 복잡도 : O(n + k)
이론적으로 기수 정렬은 모든 비교 정렬보다 빠르다.
하지만, 항목의 길이 k가 매우 길어질 경우 무시할 수 없으므로 논란의 여지가 있다.
무작위로 분산된 데이터를 다룰 때는 k가 log n 이 되어 시간 복잡도가 O(n log n)이 되고, 그러면 비교 정렬의 속도와 비슷해질 수도 있다.
